题目内容
11. 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.(1)求点B的坐标;
(2)求OA:0B的值;
(3)若点A在双曲线上移动,保持OA⊥0B不变,OA:OB的值变吗?
分析 (1)过A作AC垂直于y轴,过B作BD垂直于y轴,利用垂直的定义可得出一对直角相等,再由OA与OB垂直,利用平角的定义得到一对角互余,在直角三角形AOC中,两锐角互余,利用同角的余角相等得到一对角相等,利用两对对应角相等的三角形相似得到三角形AOC与三角形OBD相似,利用反比例函数k的几何意义求出两三角形的面积,得出面积比,利用面积比等于相似比的平方求出相似比,即$\frac{OC}{BD}=\frac{AC}{OD}$的比值,可得BD、OD,易得点B的坐标;
(2)由(1)利用面积比等于相似比的平方求出相似比,即$\frac{OC}{BD}=\frac{AC}{OD}$=$\frac{OA}{OB}$;
(3)因为S△AOC、S△BOD不变,利用利用面积比等于相似比的平方求出相似比,可得结论.
解答 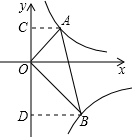 解:(1)过A作AC⊥y轴,过B作BD⊥y轴,可得∠ACO=∠BDO=90°,
解:(1)过A作AC⊥y轴,过B作BD⊥y轴,可得∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵OA⊥OB,
∴∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∵点A、B分别在反比例函数y=$\frac{2}{x}$(x>0),y=-$\frac{6}{x}$(x>0)的图象上,
∴S△AOC=1,S△OBD=3,
∴S△AOC:S△OBD=1:3,
$\frac{OC}{BD}=\frac{AC}{OD}=\sqrt{\frac{{S}_{△ACO}}{{S}_{ODB}}}=\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$,
即$\frac{2}{BD}=\frac{1}{OD}=\frac{\sqrt{3}}{3}$,
∴$BD=2\sqrt{3}$,OD=$\sqrt{3}$,
∴B(2$\sqrt{3}$,-$\sqrt{3}$);
(2)OA:OB=OC:BD=$\sqrt{3}$:3;
(3)不变.
∵点A在y=$\frac{2}{x}$上运动时,S△AOC=1,S△BOD=3,
∴$\frac{OA}{OB}=\frac{\sqrt{3}}{3}$
点评 本题主要考查了反比例函数图象上点的坐标的特征,相似三角形的性质及判定,利用面积比等于相似比的平方是解答此题的关键.

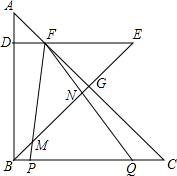 如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$.
如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$.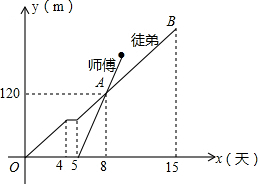 为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.
为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题. 如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.
如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.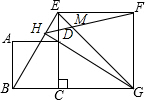 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.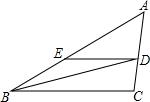 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.