题目内容
18．
如图，将一张长方形纸片的一角斜折过去，使角的顶点A落在A′处，BC为折痕，若BD平分∠A′BE，则BC与BD的位置关系是垂直．
分析 根据折叠前后角相等的性质，平角的定义求解即可．
解答 解：∵将一张长方形纸片的一角斜折过去，使角的顶点A落在A′处，BC为折痕，
∴∠ABC=∠A′BC=$\frac{1}{2}$∠ABA′，
∵BD平分∠A′BE，
∴∠A′BD=∠EBD=$\frac{1}{2}$∠A′BE，
∴∠CBD=∠CBA′+∠A′BD=$\frac{1}{2}$（∠ABA′+∠A′BE）=$\frac{1}{2}$×180°=90°，
∴BC与BD垂直，
故答案为：垂直．
点评 本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
15．
如图，AOB是一条直线，∠AOD=∠EOC=∠DOB=90°，那么互为补角的角共有（ ）
如图，AOB是一条直线，∠AOD=∠EOC=∠DOB=90°，那么互为补角的角共有（ ）| A． | 3对 | B． | 4对 | C． | 6对 | D． | 7对 |
9．化简$\sqrt{2}$+（$\sqrt{2}$-1）的结果是（ ）
| A． | $2\sqrt{2}-1$ | B． | $2-\sqrt{2}$ | C． | $1-\sqrt{2}$ | D． | $2+\sqrt{2}$ |
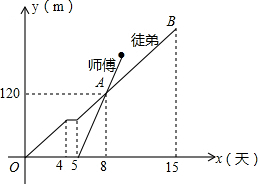为了检修自来水管道，由师徒两人完成，两人从管道两端开始检修，已知徒弟先修了4天后，休息了1天，接着师徒两人合做了5天，师傅被安排做其他工作，余下由徒弟单独检修完，如图是师傅和徒弟修管道的长度与工作时间的函数图象，请根据图象提供的信心解答下列问题．
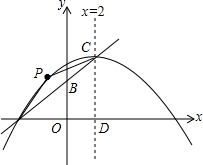在平面直角坐标系中，A（-4，0），B（0，2），直线x=2与直线AB交于点C，与x轴交于点D，抛物线经过点A，且以C为顶点．
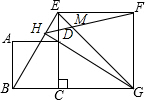如图，正方形ABCD的顶点D在正方形ECGF的边EC上，顶点B在GC的延长线上，连接EG、BE，∠EGC的平分线GH过点D交BE于H，连接HF交EG于M，则$\frac{MG}{ME}$的值为$\sqrt{2}$+1．
如图，点E为正方形ABCD中AD边上的动点，AB=2，以BE为边画正方形BEFG，连结CF和CE，则△CEF面积的最小值为$\frac{3}{2}$．