题目内容
20.等边三角形的边长为4,则它的内切圆面积等于( )| A. | 4π | B. | $\frac{4}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{16}{3}π$ |
分析 根据题意画出等边三角形ABC与内切圆O.首先根据三角形面积计算公式求出S△ABC,再观察发现三角形ABC的内切圆半径,恰好是三角形ABC内三个三角形的高,因而可以通过面积S△ABC=S△AOB+S△BOC+S△AOC来计算半径,根据面积公式计算即可.
解答 解:设⊙O与△ABC相切于D,E,F,连接CD,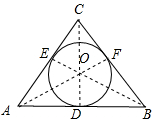
∵三角形ABC是等边三角形,
∴CD过点O,CD⊥AB,
∴CD=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$AB•CD=4$\sqrt{3}$,
设内切圆半径为r,
∴S△ABC=$\frac{1}{2}$(AB+BC+AC)r=4$\sqrt{3}$,
∴r=$\frac{2\sqrt{3}}{3}$,
∴内切圆面积=π×($\frac{2\sqrt{3}}{3}$)2=$\frac{4}{3}$π.
故选:B.
点评 本题考查了三角形的内切圆和内心,等边三角形的性质,三角形的面积,正确的画出图形是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
15.某超市预购进A,B两种品牌的书包共400个.已知两种书包的有关信息如下表所示.
(1)设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为w元.求w关于x的关系式;
(2)如果购进两种书包的总费用恰好为18000元,那么超市将所购进的两种书包全部卖出后,获得的总利润为多少元?
| 品牌 | 进价(元/个) | 售价(元/个) |
| A | 47 | 65 |
| B | 37 | 50 |
(2)如果购进两种书包的总费用恰好为18000元,那么超市将所购进的两种书包全部卖出后,获得的总利润为多少元?
12.下列不等式一定成立的是( )
| A. | a<2a | B. | a<a+2 | C. | -a>-2a | D. | a+2>2 |
9.一次函数y=kx+b过点(-2,5),且它的图象与y轴的交点和直线y=-$\frac{1}{2}$x-3与y轴的交点相同,那么一次函数的解析式是( )
| A. | y=-4x-3 | B. | y=-4x+3 | C. | y=4x-3 | D. | y=4x+3 |
10.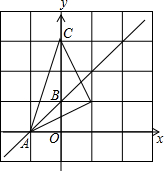 如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )
如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )
 如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )
如图,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是( )| A. | (0,1) | B. | (0,-3) | C. | (3,0) | D. | (2,1) |
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为2.
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为2.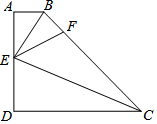 如图,在四边形ABCD中,AB∥CD,∠D=90°,E为AD上一点,分别以EB,EC为折痕将这两个角(∠A,∠D)向内折起,点A,D恰好落在BC边的F处,若AB=1,DC=4,则△EBC的面积为5.
如图,在四边形ABCD中,AB∥CD,∠D=90°,E为AD上一点,分别以EB,EC为折痕将这两个角(∠A,∠D)向内折起,点A,D恰好落在BC边的F处,若AB=1,DC=4,则△EBC的面积为5. 作图题(要求尺规作图,保留作图痕迹,不写作法)
作图题(要求尺规作图,保留作图痕迹,不写作法)