题目内容
9.一次函数y=kx+b过点(-2,5),且它的图象与y轴的交点和直线y=-$\frac{1}{2}$x-3与y轴的交点相同,那么一次函数的解析式是( )| A. | y=-4x-3 | B. | y=-4x+3 | C. | y=4x-3 | D. | y=4x+3 |
分析 将x=0代入直线y=-$\frac{1}{2}$x-3中即可求出一次函数y=kx+b的图象与y轴的交点坐标,再根据点的坐标利用待定系数法即可求出一次函数的解析式,此题得解.
解答 解:当x=0时,y=-$\frac{1}{2}$x-3=-3,
∴点(0,-3)在一次函数y=kx+b的图象上.
将(-2,5)、(0,-3)代入y=kx+b,
$\left\{\begin{array}{l}{-2k+b=5}\\{b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-4}\\{b=-3}\end{array}\right.$,
∴一次函数的解析式为y=-4x-3.
故选A.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及待定系数法求一次函数解析式,根据点的坐标利用待定系数法求出一次函数的解析式是解题的关键.

练习册系列答案
相关题目
20.等边三角形的边长为4,则它的内切圆面积等于( )
| A. | 4π | B. | $\frac{4}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{16}{3}π$ |
1.下列单项式系数相同的是( )
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③ |
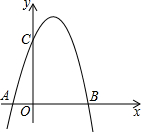 如图,对称轴为直线x=$\frac{1}{2}$的抛物线经过B(2,0),C(0,4)两点,抛物线与x轴的另一交点为A.
如图,对称轴为直线x=$\frac{1}{2}$的抛物线经过B(2,0),C(0,4)两点,抛物线与x轴的另一交点为A.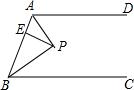 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6. 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,当对角线AC,BD满足什么条件时,四边形EFGH是菱形?请说明理由.
如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,当对角线AC,BD满足什么条件时,四边形EFGH是菱形?请说明理由.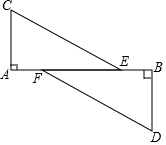 如图,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度行驶最终同时到达A、B两点,那么CE与DF平行吗?为什么?
如图,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度行驶最终同时到达A、B两点,那么CE与DF平行吗?为什么? 已知:P是边长为4厘米的正方形ABCD的边BC上的点,且PC=1厘米,M是CD边上的一个动点,
已知:P是边长为4厘米的正方形ABCD的边BC上的点,且PC=1厘米,M是CD边上的一个动点,