题目内容
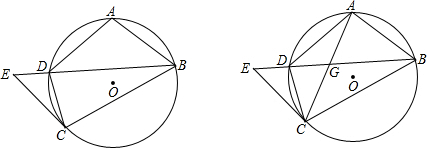
18.已知:四边形ABCD内接于⊙O,点A是弧BD的中点,过点C作⊙O的切线交弦BD的延长线于E.(1)求证:∠DCE=∠CBD;
(2)弦AC和弦BD相交于点G,求证:EG=EC.
分析 (1)根据弦切角定理证明即可;
(2)根据弦、弧、圆心角的关系得到∠DCA=∠BCA,根据三角形的外角的性质、等腰三角形的判定定理证明.
解答 证明:(1)∵CE是⊙O的切线,
∴由弦切角定理得,∠DCE=∠CBD;
(2)∵点A是弧BD的中点,
∴∠DCA=∠BCA,
又∠DCE=∠CBD,
∴∠DCA+∠DCE=∠BCA+∠CBD,即∠ECG=∠EGC,
∴EG=EC.
点评 本题考查的是切线的性质、圆内接四边形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
8.计算|-$\frac{3}{2}$|+1的结果是( )
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
7. 如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )
如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )
 如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )
如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )| A. | c<a<b | B. | a<b<c | C. | a<c<b | D. | c<b<a |
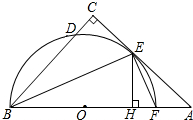 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆. 如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)
如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)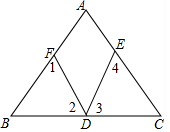 如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.
如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.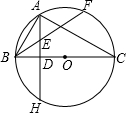 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6