题目内容
7.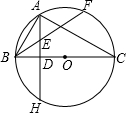 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6(1)求证:AE=BE;
(2)求DE、BD的长.
分析 (1)连接AF,根据圆周角定理求得;
(2)设DE=x(x>0),由AD=6,BE•EF=32,AE•EH=BE•EF,可列式为(6-x)(6+x)=32,由(1)知BE=AE=6-2=4,根据Rt△BDE中的勾股定理求解.
解答 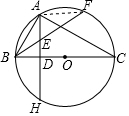 (1)证明:连AF,
(1)证明:连AF,
∵A是$\widehat{BF}$的中点,
∴∠ABE=∠AFB.
又∠AFB=∠ACB,
∴∠ABE=∠ACB.
∵BC为直径,
∴∠BAC=90°,AH⊥BC.
∴∠BAE=∠ACB.
∴∠ABE=∠BAE.
∴AE=BE.
(2)解:设DE=x(x>0),由AD=6,BE•EF=32,AE•EH=BE•EF,
则(6-x)(6+x)=32,
解得x=2,即DE的长为2;
由(1)得BE=AE=6-2=4,
在Rt△BDE中,BD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 此题主要考查的是圆周角定理,勾股定理,垂径定理的运用.牢固掌握该定理可在综合题型中灵活运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
17.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | x8÷x2=x6 | C. | (ab3)2=ab6 | D. | (x+2)2=x2+4 |
15.下列运算中,正确的是( )
| A. | x3•x2•x=x5 | B. | x2+x2=2x4 | C. | (2x)2=2 x4 | D. | (x+m)(x-m)=x2-m2 |
2.△ABC中,∠C=90°,sinA=$\frac{{2\sqrt{2}}}{3}$,则tanA的值是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
16.科学家在实验中检测出某微生物约为0.0000025米,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 2.5×106 | C. | 2.5×10-5 | D. | 25×10-5 |