题目内容
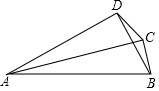
7. 如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )
如图,每个小正方形的边长为1,△ABC的三边a、b、c的大小关系式正确的是( )| A. | c<a<b | B. | a<b<c | C. | a<c<b | D. | c<b<a |
分析 通过小正方形网格,可以看出AB=4,AC、BC分别可以构造直角三角形,再利用勾股定理可分别求出b、a,然后比较三边的大小即可.
解答 解:∵b=AC=$\sqrt{{4}^{2}+{3}^{2}}$=5=$\sqrt{25}$,a=BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,c=4=$\sqrt{16}$,
∴b>a>c,
即c<a<b.
故选A.
点评 本题考查了勾股定理,由勾股定理求出a、b的长是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.科学家在实验中检测出某微生物约为0.0000025米,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 2.5×106 | C. | 2.5×10-5 | D. | 25×10-5 |
12.点A在数轴上到原点的距离为5,则A点表示的数为( )
| A. | 5 | B. | -5 | C. | 10 | D. | 5或-5 |
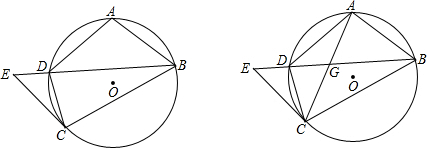
 如图,在四边形ABCD中,∠ACB=∠ADB=90°,且AC平分∠BAD.
如图,在四边形ABCD中,∠ACB=∠ADB=90°,且AC平分∠BAD.