题目内容
13. 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆上的三等分点,则图中阴影部分的面积等于$\frac{25π}{6}$.
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆上的三等分点,则图中阴影部分的面积等于$\frac{25π}{6}$.
分析 连接CO,DO,利用等底等高的三角形面积相等可知S阴影=S扇形COD,利用扇形的面积公式计算即可.
解答  解:连接CO,DO,
解:连接CO,DO,
∵C,D是以AB为直径的半圆上的三等分点,
∴∠COD=60°,
∵△PCD的面积等于△OCD的面积,
∴都加上CD之间弓形的面积得出S阴影=S扇形OCD=$\frac{60π•{5}^{2}}{360}$=$\frac{25π}{6}$,
故答案为:$\frac{25π}{6}$.
点评 本题考查了扇形面积的计算.根据图形推知图中阴影部分面积=扇形OCD的面积是解题的关键.

练习册系列答案
相关题目
5.若直线y=kx+2经过第一、二、四象限,则函数y=$\frac{2}{kx}$的图象在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
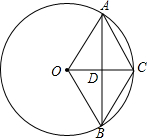 如图,已知OC是⊙O的半径,过OC的中点D作DC的垂线交⊙O于点A,B,以下结论:
如图,已知OC是⊙O的半径,过OC的中点D作DC的垂线交⊙O于点A,B,以下结论: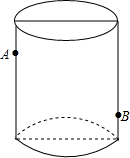 如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)
如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)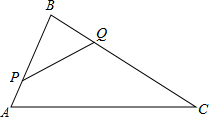 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?