题目内容
4.在△ABC中,∠A,∠B都是锐角,且满足|sinA-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠C的度数为105°.分析 由非负数的性质可知:sinA=$\frac{\sqrt{2}}{2}$,cosB=$\frac{\sqrt{3}}{2}$,从而可求得∠A,∠B的度数,然后由三角形的内角和定理可求得∠C的度数.
解答 解:∵|sinA-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,
∴sinA=$\frac{\sqrt{2}}{2}$,cosB=$\frac{\sqrt{3}}{2}$.
∴∠A=45°,∠B=30°.
由三角形的内角和是180°可知∠C=180°-30°-45°=105°.
故答案为:105°.
点评 本题主要考查的是特殊锐角三角函数值、三角形的内角和定理、非负数的性质的应用,求得∠A,∠B的度数是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
12.有下面4个命题:
①直径相等的两个圆是等圆;
②长度相等的弧是等弧;
③圆中最长的弦是通过圆心的弦;
④一条弦把圆分成两条弧,这两条弧不可能是等弧,
其中真命题的个数为( )
①直径相等的两个圆是等圆;
②长度相等的弧是等弧;
③圆中最长的弦是通过圆心的弦;
④一条弦把圆分成两条弧,这两条弧不可能是等弧,
其中真命题的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.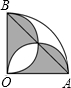 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )| A. | πcm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{1}{2}$cm2 | D. | $\frac{2}{3}$cm2 |
 如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?



 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆上的三等分点,则图中阴影部分的面积等于$\frac{25π}{6}$.
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆上的三等分点,则图中阴影部分的面积等于$\frac{25π}{6}$.