题目内容
15. 如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交梯形的对角线OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△AOC=15,则图中阴影部分(S△EBO+S△ACD)的面积为( )
如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=$\frac{k}{x}$的一支在第二象限交梯形的对角线OC于点D,交边BC于点E,且$\frac{OD}{CD}$=2,S△AOC=15,则图中阴影部分(S△EBO+S△ACD)的面积为( )| A. | 18 | B. | 17 | C. | 16 | D. | 15 |
分析 设D(m,$\frac{k}{m}$),根据$\frac{OD}{CD}$=2表示出B、C的横坐标为$\frac{3}{2}$m,再代入解析式求出A的横坐标,利用△AOC的面积公式求出k的值,从而计算出阴影部分面积.
解答 解:设D(m,$\frac{k}{m}$),
∵$\frac{OD}{CD}$=2,
∴B、C的横坐标为$\frac{3}{2}$m,
A、C的纵坐标为$\frac{3}{2}$•$\frac{k}{m}$=$\frac{3k}{2m}$,
∴A的横坐标x=k÷$\frac{3k}{2m}$=$\frac{2m}{3}$,
∴AC=$\frac{2m}{3}$-$\frac{3}{2}$m=-$\frac{5}{6}$m,
∴S△AOC=$\frac{1}{2}$AC•BC
=$\frac{1}{2}$(-$\frac{5}{6}$m)•$\frac{3k}{2m}$=-$\frac{5}{8k}$=15,
∴k=-24,
∴S△EBO=$\frac{1}{2}$|k|=12,S△ACD=$\frac{1}{2}$S△ACO=5,
∴S阴影=S△EBO+S△ACD=17.
故选B.
点评 本题考查的是反比例函数系数k的几何意义,先设出D的坐标,再用m表示出各点坐标,利用三角形的面积求解是解答此题的关键.

练习册系列答案
相关题目
5. 如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )
 如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )| A. | S矩形AMKP=S矩形KQCN | |
| B. | S${\;}_{矩{形}_{MBQK}}$>S矩形PKND | |
| C. | S矩形AMKP>S矩形KQCN | |
| D. | S矩形AMKP+S矩形KQCN=S矩形MBQK+S矩形PKND |
 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段EC的长度是( )
如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段EC的长度是( ) 如图所示的双曲线是函数y=-$\frac{k}{x}$(x<0)和y=$\frac{4}{x}$(x>0)的图象,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,点C是x轴上任意一点,连接CP、CQ,若△CPQ的面积是3,则k的值是2.
如图所示的双曲线是函数y=-$\frac{k}{x}$(x<0)和y=$\frac{4}{x}$(x>0)的图象,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,点C是x轴上任意一点,连接CP、CQ,若△CPQ的面积是3,则k的值是2.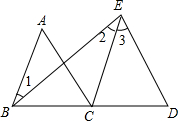 如图:∠1=∠2,∠A=∠3,求证:AC∥DE.
如图:∠1=∠2,∠A=∠3,求证:AC∥DE.