题目内容
10. 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{5}$ |
分析 根据菱形的性质可得点B与点D关于直线AC对称,连接BE与AC相交于点P,根据轴对称确定最短路线问题,BE的长度即为PE+PD的最小值,连接BD,根据菱形的性质求出∠BCD=60°,从而判断出△BCD是等边三角形,再根据等边三角形的性质求出BE的长度即可.
解答 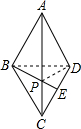 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴点B与点D关于直线AC对称,
如图,连接BE与AC相交于点P,由轴对称确定最短路线问题,BE的长度即为PE+PD的最小值,
连接BD,∵∠B=120°,
∴∠BCD=180°-120°=60°,
又∵BC=CD,
∴△BCD是等边三角形,
∵E是CD的中点,
∴BE=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
即PE+PD的最小值为2$\sqrt{3}$.
故选B.
点评 本题考查了轴对称确定最短路线问题,菱形的性质,等边三角形的判定与性质,熟记各性质并准确确定出点P的位置是解题的关键.

练习册系列答案
相关题目
1.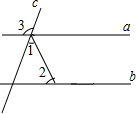 如图,直线a,直线b被直线c所截,且a∥b,若∠1=52°,∠2=61°,则∠3的度数为( )
如图,直线a,直线b被直线c所截,且a∥b,若∠1=52°,∠2=61°,则∠3的度数为( )
 如图,直线a,直线b被直线c所截,且a∥b,若∠1=52°,∠2=61°,则∠3的度数为( )
如图,直线a,直线b被直线c所截,且a∥b,若∠1=52°,∠2=61°,则∠3的度数为( )| A. | 104° | B. | 113° | C. | 115° | D. | 120° |
19.把方程-2x=4的未知数系数化1,得( )
| A. | x=4 | B. | x=-4 | C. | x=2 | D. | x=-2 |
 如图,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E,使BE=BD,过点D,E引直线交AC于点F.
如图,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E,使BE=BD,过点D,E引直线交AC于点F. 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△ADC=9,则k=6.
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△ADC=9,则k=6.