题目内容
15. 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△ADC=9,则k=6.
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△ADC=9,则k=6.
分析 先作AD⊥x轴于D,BE⊥x轴于E,根据得A、B两点的横坐标求得纵坐标,再证明△CEB∽△CDA,利用相似三角形的性质得出DE=CE,由OD:OE=a:2a=1:2,得出OD=DE,所以D是OC的三等分点,进而得到S△AOD=$\frac{1}{3}$S△AOC=3,然后利用反比例函数系数k的几何意义,求得k的值.
解答  解:如图,作AD⊥x轴于D,BE⊥x轴于E,
解:如图,作AD⊥x轴于D,BE⊥x轴于E,
∵A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,
∴A、B两点的纵坐标分别是$\frac{k}{a}$、$\frac{k}{2a}$,
∵AD∥BE,
∴△CEB∽△CDA,
∴$\frac{CE}{CD}$=$\frac{BE}{AD}$=$\frac{\frac{k}{2a}}{\frac{k}{a}}$=$\frac{1}{2}$,
∴DE=CE,
∵OD:OE=a:2a=1:2,
∴OD=DE,
∴OD=$\frac{1}{3}$OC,
∴S△AOD=$\frac{1}{3}$S△AOC=$\frac{1}{3}$×9=3,
∴$\frac{1}{2}$|k|=3,即k=±6,
而k>0,
∴k=6.
故答案为:6.
点评 本题主要考查了反比例函数中比例系数k的几何意义以及相似三角形的判定与性质,解题时注意:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
相关题目
6.抛物线y=-2x2-6x+1与x轴的交点个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10. 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{5}$ |
7.用下列同一种多边形瓷砖铺设地平面,不能铺满地平面的是( )
| A. | 正三角形瓷砖 | B. | 长方形瓷砖 | C. | 正五边形瓷砖 | D. | 正六边形瓷砖 |
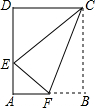 如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$.
如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$. 如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是∠ABC=∠DCB或AC=DB.
如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是∠ABC=∠DCB或AC=DB.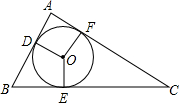 如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.
如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.