题目内容
20. 如图,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E,使BE=BD,过点D,E引直线交AC于点F.
如图,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E,使BE=BD,过点D,E引直线交AC于点F.(1)请说明△ADF和△DFC是等腰三角形.
(2)判断AF与FC的数量关系,说明理由.
分析 根据等边对等角可得∠E=∠BDE,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ABC=2∠BDE,从而求出∠C=∠BDE,再求出∠C=∠CDF,然后根据等角对等边求出DF=FC,再根据等角的余角相等求出∠CAD=∠ADF,根据等角对等边求出DF=AF,即可得到AF=FC.
解答 (1)证明:∵BE=BD,
∴∠E=∠BDE,
∵∠ABC=∠E+∠BDE=2∠BDE,∠ABC=2∠C,
∴∠C=∠BDE,
又∵∠BDE=∠CDF,
∴∠C=∠CDF,
∴DF=FC,
∴△DFC为等腰三角形;
∵AD为BC边上的高,
∴∠CDF+∠ADF=∠ADC=90°,
∠C+∠CAD=180°-90°=90°,
∴∠CAD=∠ADF,
∴DF=AF,
∴△ADF是等腰三角形;
(2)解:由(1)知AF=DF=FC.
点评 本题考查了等腰三角形的判定与性质,等角的余角相等的性质,本题的关键是得到∠FDC=∠C..

练习册系列答案
相关题目
10.每年的12月2日为我国的交通安全日,下列交通图标是轴对称图形的共有( )

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.在反比例函数y=-$\frac{1}{x}$的图象上有三点A(-2,a),B(-1,b),C(3,c),则a,b,c的大小关系是( )
| A. | b<c<a | B. | c<a<b | C. | c<b<a | D. | a<b<c |
15.一次抽奖活动中,印发100张奖券,其中一等奖5张,二等奖10张,三等奖20张,一位抽奖者仅买一张奖券,中奖的可能性为( )
| A. | $\frac{7}{20}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{20}$ |
12.若将方程x2+16x+57=0化成(x+a)2=b的形式,则a,b的值分别是( )
| A. | a=7,b=8 | B. | a=8,b=7 | C. | a=-7,b=-8 | D. | a=-8,b=-7 |
10. 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{5}$ |
 如图,求等腰三角形ABC的面积.
如图,求等腰三角形ABC的面积.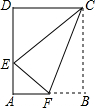 如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$.
如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$.