题目内容
19.把方程-2x=4的未知数系数化1,得( )| A. | x=4 | B. | x=-4 | C. | x=2 | D. | x=-2 |
分析 在等式的两边同时除以-2即可.
解答 解:由原方程得到:$\frac{-2}{-2}$x=$\frac{4}{-2}$,即x=-2.
故选:D.
点评 本题考查了一元一次方程的解的.把方程的解代入原方程,等式左右两边相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
 如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是4,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{5}$ |
7.用下列同一种多边形瓷砖铺设地平面,不能铺满地平面的是( )
| A. | 正三角形瓷砖 | B. | 长方形瓷砖 | C. | 正五边形瓷砖 | D. | 正六边形瓷砖 |
14.已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
则下列判断中正确的是( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -5 | 1 | 3 | 1 | … |
| A. | 抛物线开口向上 | |
| B. | 抛物线与y轴交于负半轴 | |
| C. | 当x=4时,y>0 | |
| D. | 方程ax2+bx+c=0的正根为α,则2<α<3 |
11.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=6}\\{2y+z=4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=4}\\{x-y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=5}\\{{x}^{2}+{y}^{2}=13}\end{array}\right.$ |
8.下列四个等式从左至右的变形中,是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | x2-2xy+y2-z2=(x-y)2-z2 | ||
| C. | ab-a-b+1=(a-1)(b-1) | D. | m2-2m-3=m(m-2-$\frac{3}{m}$) |
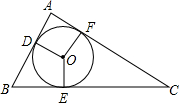 如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.
如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.