题目内容
18.如图,已知B是线段AC上的一点,M是线段AB的中点,N是线段AC的中点,P为NA的中点,Q是AM的中点,则MN:PQ等于多少?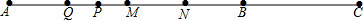
分析 根据线段中点的性质,可得AQ=QM=$\frac{AM}{2}$=$\frac{AB}{4}$,AP=NP=$\frac{AN}{2}$=$\frac{AC}{4}$,根据线段的和差,可得MN,PQ,根据比的性质,可得答案.
解答 解:如图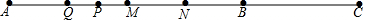 ,
,
∵M是AB的中点,
∴AM=BM=$\frac{AB}{2}$.
∵Q是MA的中点,
∴AQ=QM=$\frac{AM}{2}$=$\frac{AB}{4}$.
∵N是AC的中点,
∴AN=CN=$\frac{AC}{2}$.
∵P是NA的中点,
∴AP=NP=$\frac{AN}{2}$=$\frac{AC}{4}$,
∴MN=AN-AM=$\frac{AC}{2}$-$\frac{AB}{2}$=$\frac{AC-AB}{2}$,
PQ=AP-AQ=$\frac{AC}{4}$-$\frac{AB}{4}$=$\frac{AC-AB}{4}$,
∴MN:PQ=$\frac{AC-AB}{2}$:$\frac{AC-AB}{4}$=2:1.
点评 本题考查了两点间的距离,利用线段中点的性质、线段的和差得出MN,PQ是解题关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
13.若方程(m-1)${x^{{m^2}+1}}$-x+3=0是关于x的一元二次方程,那么m的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 以上都不对 |
8.有一列数a1、a2、a3、…an,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=-1,则a2013=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 2012 |
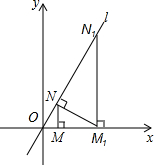 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).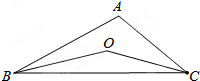 如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.
如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.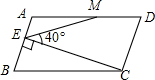 如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.