Question

10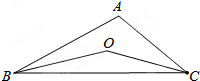．如图，BO、CO分别平分∠ABC、∠ACB，∠A=100°，则∠BOC的度数为140°．

Answer 1

分析 根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数，再根据三角形的内角和定理即可求出∠BOC的度数．

解答 解：∵OB、OC分别是∠ABC和∠ACB的角平分线，
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$（∠ABC+∠ACB），
∵∠A=100°，
∴∠OBC+∠OCB=$\frac{1}{2}$（180°-100°）=40°，
∴∠BOC=180°-（∠OBC+∠OCB）
=180°-40°
=140°．
故答案为：140°

点评 本题主要利用角平分线的定义和三角形内角和定理求解，熟记概念和定理是解题的关键．