题目内容
4.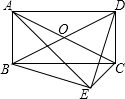 如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.
如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.
分析 连接EO,首先根据平行四边形的性质可得AO=CO,BO=DO,即O为BD和AC的中点,在Rt△AEC中EO=$\frac{1}{2}$AC,在Rt△EBD中,EO=$\frac{1}{2}$BD,进而得到AC=BD,再根据对角线相等的平行四边形是矩形可证出结论.
解答 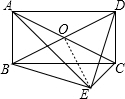 证明:连接EO,
证明:连接EO,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
在Rt△EBD中,
∵O为BD中点,
∴EO=$\frac{1}{2}$BD,
在Rt△AEC中,∵O为AC中点,
∴EO=$\frac{1}{2}$AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
14.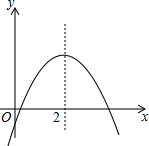 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.(-a2)3=( )
| A. | a5 | B. | a6 | C. | -a5 | D. | -a6 |
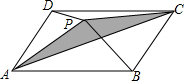 如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.
如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3. 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.