题目内容
19.解方程(组):(1)$\left\{\begin{array}{l}2x+y=10\\ x=2y\end{array}\right.$
(2)$\left\{\begin{array}{l}2s-3t=4\\ 5s-3t=19\end{array}\right.$
(3)x(x+2)=(x-2)(x-3)
(4)(x+2)(x-2)=(x+2)2.
分析 (1)先把x=2y代入2x+y=10中,即可求出y的值,再把y的值代入原方程即可求出x的值.
(2)本题y的系数相同,可考虑直接用减法消去t.
(3)此题可先将括号去掉,然后再移项、合并同类项,系数化1即可得出x的值.
(4)先移项,再把x+2作为整体,提公因式即可.
解答 解:(1)$\left\{\begin{array}{l}2x+y=10\\ x=2y\end{array}\right.$
解:把x=2y代入2x+y=10中,
得4y+y=10,
整理得5y=10,
∴y=2,
把y=2代入原方程得:x=4,
∴原方程组的解$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{2s-3t=4①}\\{5s-3t=19②}\end{array}\right.$
①-②,得
-3s=-15,
s=5,
把s=5代入①,得
10-3t=4,
t=2,
∴原方程组的解为:$\left\{\begin{array}{l}{s=5}\\{t=2}\end{array}\right.$.
(3)x(x+2)=(x-2)(x-3)
整理得,2x=-5x+6,
7x=6,
x=$\frac{6}{7}$.
(4)(x+2)(x-2)=(x+2)2.
移项得,(x+2)(x-2)-(x+2)2=0
提公因式得,(x+2)(x-2-x-2)=0,
即x+2=0,
解得x=-2.
点评 本题考查了二元一次方程组的解法主要运用了代入法和加减法消元法,也考查了用因式分解法解一元二次方程,是基础知识要熟练掌握.

练习册系列答案
相关题目
10.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
14.(x+a)(x-3)的积的常数项是15,则a的值是( )
| A. | 12 | B. | 5 | C. | -5 | D. | -12 |
9.学校春游,如果每辆汽车坐45人,则有28人没有上车;如果每辆坐50人,则空出一辆汽车,并且有一辆车还可以坐12人,设有x辆汽车,可列方程( )
| A. | 45x-28=50(x-1)-12 | B. | 45x+28=50(x-1)+12 | C. | 45x+28=50(x-1)-12 | D. | 45x-28=50(x-1)+12 |
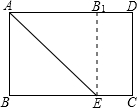 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.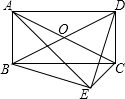 如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.
如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.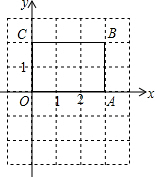 如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、C(0,2),点B在第一象限.
如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、C(0,2),点B在第一象限.