题目内容
15.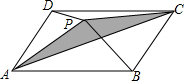 如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.
如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.
分析 根据图形得出S△PAB+S△PCD=S△ADC,求出S△ADC-S△PCD=S△PAB,求出S△PAC=S△PAB-S△PAD,代入求出即可.
解答 解:∵S△PAB+S△PCD=$\frac{1}{2}$S平行四边形ABCD=S△ADC,
∴S△ADC-S△PCD=S△PAB,
则S△PAC=S△ACD-S△PCD-S△PAD
=S△PAB-S△PAD
=8-5
=3.
故答案为:3.
点评 本题考查了平行四边形的性质、平行四边形的面积、三角形面积;解决问题的关键是推出S△PAC=S△PAB-S△PAD.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )
| A. | $\frac{5}{18}$ | B. | $\frac{5}{16}$ | C. | $\frac{13}{15}$ | D. | $\frac{12}{13}$ |
10.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
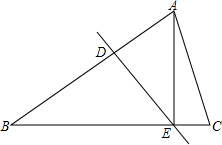 如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E
如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E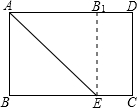 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为2cm.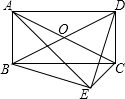 如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.
如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.