题目内容
13.对于四边形的以下说法:其中正确的个数有( )①对角线互相平分的四边形是平行四边形;
②对角线相等且互相平分的四边形是矩形;
③对角线垂直且互相平分的四边形是菱形;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行四边形、矩形、菱形的判定,说法正确的是①②③,顺次连接对角线相等的四边形各边的中点所得到的四边形应该是菱形.
解答 解:①两条对角线互相平分的四边形是平行四边形,属于平行四边形的判定定理,成立;
②两条对角线相等且互相平分的四边形是矩形,属于矩形的判定定理,成立;
③两条对角线互相垂直平分的四边形是菱形,属于菱形的判定定理,成立;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是菱形.不成立.
故题中①②③根据平行四边形、矩形、菱形的判定,是正确的,④只能判定是菱形而不具备矩形的条件.
故选C.
点评 本题考查特殊平行四边形的判定及中点四边形的判定,注意中点四边形的形状与原四边形的对角线有关:一般四边形的中点四边形为平行四边形;若原四边形的对角线相等,则中点四边形为菱形;若原四边形的对角线垂直,则中点四边形为矩形;若原四边形的对角线相等且互相垂直,则中点四边形为正方形形.

练习册系列答案
相关题目
3.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )
| A. | $\frac{5}{18}$ | B. | $\frac{5}{16}$ | C. | $\frac{13}{15}$ | D. | $\frac{12}{13}$ |
1.一元二次方程x(x-2)=0根的情况是( )
| A. | 只有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
18.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c三边,则下列式子一定成立的是( )
| A. | a=c•sinB | B. | a=c•cosB | C. | $c=\frac{a}{tanB}$ | D. | c=a•sinA |
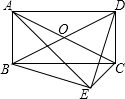 如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.
如图,平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°,试说明:四边形ABCD是矩形.