题目内容
12.(1)解方程组$\left\{\begin{array}{l}{\frac{x}{4}-y=-1}\\{x=3y}\end{array}\right.$,(2)解不等式组:$\left\{\begin{array}{l}{x-3(x-2)>4}\\{\frac{2x-1}{5}≥\frac{x+1}{2}}\end{array}\right.$.
分析 (1)先用代入消元法求出y的值,再求出x的值即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)$\left\{\begin{array}{l}\frac{x}{4}-y=-1①\\ x=3y②\end{array}\right.$,把②代入①得,$\frac{3y}{4}$-y=-1,解得y=4,
把y=4代入②得,x=12,
故原方程组的解为:$\left\{\begin{array}{l}x=12\\ y=4\end{array}\right.$;
(2)$\left\{\begin{array}{l}x-3(x-2)>4①\\ \frac{2x-1}{5}≥\frac{x+1}{2}②\end{array}\right.$,由①得,x<1,由②得,x≤-7,
故不等式组的解集为:x≤-7.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
2.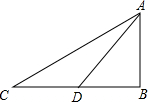 如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
 如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )| A. | 100($\sqrt{3}$+1)米 | B. | 100米 | C. | 100$\sqrt{2}$ | D. | 200$\sqrt{3}$ |
17.在实数$\frac{22}{7}$,3.14,$\root{3}{4}$,$\sqrt{3}$,$\root{3}{-8}$,$\frac{π}{3}$,0.2020020002…(每两个相邻的2中间依次多一个0)中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.2016年1月19日,国家统计局公布了2015年宏观经济数据,初步核算,全年国内生产总值为676000亿元.676000用科学记数法表示为( )
| A. | 6.76×106 | B. | 6.76×105 | C. | 67.6×105 | D. | 0.676×106 |
2.若一组数据3,x,4,5,6的众数是3,则这组数据的中位数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |