题目内容
16.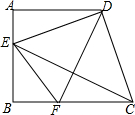 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.(1)求证:DE=DC;
(2)如果BE2=BF•BC,求证:∠BEF=∠CEF.
分析 (1)过D作DG⊥BC于G,构造成矩形,然后通过三角形全等得到结论.
(2)根据等腰三角形的性质三线合一,证得线段的垂直平分线,由等边对等角得到∠FEC=∠FCE,通过三角形相似得到∠BEF=∠FCE,于是得出∠BEF=∠CEF.
解答 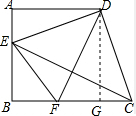 (1)证明:过D作DG⊥BC于G,
(1)证明:过D作DG⊥BC于G,
∵AD∥BC,∠A=90°,
∴∠B=90°,
∴四边形ABGD是矩形,
∴∠ADG=90°,DG=AB,
∵∠EDC=90°,
∴∠ADE=∠CDG,
在△AED与△GCD中,
$\left\{\begin{array}{l}{∠A=∠DGC}\\{AD=DG}\\{∠ADE=∠GDC}\end{array}\right.$,
∴△AED≌△GCD,
∴DE=CD;
(2)由(1)知:DE=CD,
∵DF平分∠EDC,
∴DF⊥CE,
∴EF=CF,
∴∠FEC=∠FCE,
∵BE2=BF•BC,
∴$\frac{BE}{BF}$=$\frac{BC}{BE}$,∵∠B=∠B,
∴△EFB∽△CEB,
∴∠BEF=∠FCE,
∴∠BEF=∠CEF.
点评 本题考查了矩形的判定和性质,全等三角形的判定与性质,线段的垂直平分线的性质,相似三角形的判定和性质,辅助线的作法是解题的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
4. 如图所示,正四棱锥的俯视图为( )
如图所示,正四棱锥的俯视图为( )
 如图所示,正四棱锥的俯视图为( )
如图所示,正四棱锥的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
1.算式(2+1)•(22+1)•(24+1)…(232+1)+1计算结果的个位数字是( )
| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
5.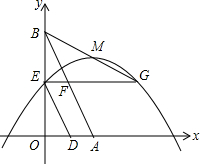 已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
 已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )| A. | -$\frac{\sqrt{3}}{3}$、$\frac{2\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$、$\frac{3\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$、$\frac{3\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{3}}{4}$、$\frac{2\sqrt{3}}{3}$ |
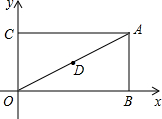 如图,在平面直角坐标系中,矩形OBAC的顶点A,B,C的坐标分别为(20,10),(20,0),(0,10).D为OA的中点,在线段OB上有一动点P,则当PA+PD为最小值时,点P的坐标是($\frac{40}{3}$,0).
如图,在平面直角坐标系中,矩形OBAC的顶点A,B,C的坐标分别为(20,10),(20,0),(0,10).D为OA的中点,在线段OB上有一动点P,则当PA+PD为最小值时,点P的坐标是($\frac{40}{3}$,0).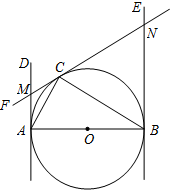 如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过 圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,求AM.
如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过 圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,求AM.