题目内容
17. 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )
如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABM中三边的关系.
解答 解:∵四边形MBND是菱形,
∴MD=MB.
∵四边形ABCD是矩形,
∴∠A=90°.
设AB=x,AM=y,则MB=2x-y,(x、y均为正数).
在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x-y)2,
解得x=$\frac{4}{3}$y,
∴MD=MB=2x-y=$\frac{5}{3}$y,
∴$\frac{AM}{MD}$=$\frac{y}{\frac{5y}{3}}$=$\frac{3}{5}$.
故选C.
点评 此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
5.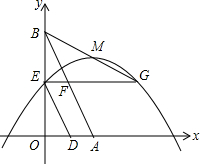 已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
 已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )
已知:如图,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点,两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动(运动到O点停止);过E点作EG∥OA交抛物线y=a(x-1)2+h(a<0)于E、G两点,交AB于点F,连结DE、BG.若抛物线的顶点M恰好在BG上且四边形ADEF是菱形,则a、h的值分别为( )| A. | -$\frac{\sqrt{3}}{3}$、$\frac{2\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$、$\frac{3\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$、$\frac{3\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{3}}{4}$、$\frac{2\sqrt{3}}{3}$ |
9. 如图,已知AB∥CD,与∠1是同位角的角是( )
如图,已知AB∥CD,与∠1是同位角的角是( )
 如图,已知AB∥CD,与∠1是同位角的角是( )
如图,已知AB∥CD,与∠1是同位角的角是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |

 如图,∠AOC:∠BOC=2:1,OD平分∠AOB,∠COD=18°,求∠AOB的度数.
如图,∠AOC:∠BOC=2:1,OD平分∠AOB,∠COD=18°,求∠AOB的度数.