题目内容
1.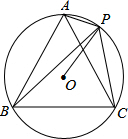 如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( )
如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①正确.根据最长的弦是直径,再根据垂径定理即可作出判断.
②错误.见图2可以说明.
③正确.根据垂径定理OP垂直平分AB,所以点C在直线OP上,由此即可证明.
④正确.根据题意点P只有在$\widehat{AC}$上,根据垂径定理即可解决问题.
解答 解:①正确.理由如下,
如图1中,
∵PB是最长的弦,
∴PB是直径,
∵AB=BC,
∴$\widehat{AB}$=$\widehat{CB}$,
∴PB⊥AC,
∴$\widehat{PA}$=$\widehat{PC}$,
∴PA=PC.
②错误,如图2中,∠PAC=30°,显然PB不是最长的弦.
③正确.如图2中,∵OP⊥AB,
∴OP垂直平分AB,
∴OP经过点C,
∴PC平分∠ACB,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACP=30°.
④正确.如图1中,∵△PAC是等腰三角形,
∴点P只有在$\widehat{AC}$上,
∵PA=PC,
∴$\widehat{PA}$=$\widehat{PC}$,
∴OP⊥AC.
故①③④正确,
故选C.
点评 本题考查三角形的外接圆、外心、垂径定理、等腰三角形的判定和性质、等边三角形的性质等知识,解题的关键是灵活应用垂径定理,掌握弧相等所对的弦相等,属于中考常考题型.

练习册系列答案
相关题目
6.一元二次方程x2-x-1=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
7.近日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位)( )
| A. | 1.2×1011 | B. | 1.3×1011 | C. | 1.26×1011 | D. | 0.13×1012 |
6.若3k+7<0,则关于x的一元二次方程x2+3x-2k=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法判断 |
10.小明解方程$\frac{1}{x}$-$\frac{x-2}{x}$=1的过程如图,他解答过程中的错误步骤是( )
解:方程两边同乘以x,得1-(x-2)=1…①
去括号,得1-x-2=1…②
合并同类项,得-x-1=1…③
移项,得-x=2…④
解得x=2…⑤
解:方程两边同乘以x,得1-(x-2)=1…①
去括号,得1-x-2=1…②
合并同类项,得-x-1=1…③
移项,得-x=2…④
解得x=2…⑤
| A. | ①②⑤ | B. | ②④⑤ | C. | ③④⑤ | D. | ①④⑤ |
11.如果点A(x1,y1),B(x2,y2)都在反比例函数y=$\frac{1}{x}$图象上,并且x1<x2<0,那么下列各式正确的是( )
| A. | y2>y1>0 | B. | y1<y2<0 | C. | y1>y2>0 | D. | y2<y1<0 |
 如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于点P(1,m ).
如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于点P(1,m ).