题目内容
4. 如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于点P(1,m ).
如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=$\frac{2}{x}$(x>0)相交于点P(1,m ).(1)求k的值;
(2)若点Q与点P关于直线y=x成轴对称,则点Q的坐标是Q(2,1);
(3)若过P、Q二点的抛物线与y轴的交点为N(0,$\frac{5}{3}$),求该抛物线的函数解析式,并求出抛物线的对称轴方程.
分析 (1)直接利用图象上点的坐标性质进而代入求出即可;
(2)连接PO,QO,PQ,作PA⊥y轴于A,QB⊥x轴于B,于是得到PA=1,OA=2,根据点Q与点P关于直线y=x成轴对称,得到直线y=x垂直平分PQ,根据线段垂直平分线的性质得到OP=OQ,根据全等三角形的性质得到QB=PA=1,OB=OA=2,于是得到结论;
(3)设抛物线的函数解析式为y=ax2+bx+c,把P、Q、N(0,$\frac{5}{3}$)代入y=ax2+bx+c,解方程组即可得到结论.
解答  解:(1)∵直线y=kx+1与双曲线y=$\frac{2}{x}$(x>0)交于点A(1,m),
解:(1)∵直线y=kx+1与双曲线y=$\frac{2}{x}$(x>0)交于点A(1,m),
∴m=2,
把A(1,2)代入y=kx+1得:k+1=2,
解得:k=1;
(2)连接PO,QO,PQ,作PA⊥y轴于A,QB⊥x轴于B,则PA=1,OA=2,
∵点Q与点P关于直线y=x成轴对称,
∴直线y=x垂直平分PQ,
∴OP=OQ,
∴∠POA=∠QOB,
在△OPA与△OQB中,
$\left\{\begin{array}{l}{∠PAO=∠OBQ}\\{∠POA=∠QOB}\\{OP=OQ}\end{array}\right.$,
∴△POA≌△QOB,
∴QB=PA=1,OB=OA=2,
∴Q(2,1);
故答案为:2,1;
(3)设抛物线的函数解析式为y=ax2+bx+c,
∵过P、Q二点的抛物线与y轴的交点为N(0,$\frac{5}{3}$),
∴$\left\{\begin{array}{l}{2=a+b+c}\\{1=4a+2b+c}\\{c=\frac{5}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=1}\\{c=\frac{5}{3}}\end{array}\right.$,
∴抛物线的函数解析式为y=-$\frac{2}{3}$x2+x+$\frac{5}{3}$,
∴对称轴方程x=-$\frac{1}{-\frac{2}{3}×2}$=$\frac{3}{4}$.
点评 本题考查了一次函数和反比例函数的交点问题,全等三角形的判定和性质,解题需把点的坐标代入函数解析式,灵活利用方程组求出所需字母的值,从而求出函数解析式,熟练掌握待定系数法求函数的解析式是解题的关键.

| A. | 2x-1+6x=3(3x+1) | B. | 2(x-1)+6x=3(3x+1) | C. | 2(x-1)+x=3(3x+1) | D. | (x-1)+x=3(x+1) |
 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 从棱长为2a的正方体零件的一角,挖去一个棱长为a的小正方体,得到一个如图所示的零件,则这个零件的俯视图是( )
从棱长为2a的正方体零件的一角,挖去一个棱长为a的小正方体,得到一个如图所示的零件,则这个零件的俯视图是( )



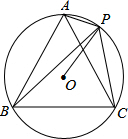 如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( )
如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( ) 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )