题目内容
6.若3k+7<0,则关于x的一元二次方程x2+3x-2k=0的根的情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法判断 |
分析 解一元一次不等式得出k的取值范围,再将其代入一元二次方程的判别式△中,找出△的值,由此即可得出结论.
解答 解:在关于x的一元二次方程x2+3x-2k=0中,
△=b2-4ac=32-4×1×(-2k)=9+8k.
∵3k+7<0,
∴k<-$\frac{7}{3}$,
∴△=9+8k<9+8×(-$\frac{7}{3}$)=-$\frac{29}{3}$.
∴关于x的一元二次方程x2+3x-2k=0无实数根.
故选A.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是找出△的值.本题属于基础题,难度不大,解决该题型题目时,通过解不等式找出k的范围,再结合根的判别式找出△的正负是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.按照山西省“改薄工程”规划,我省5年投入85亿元用于改造农村县(市、区)薄弱学校,促进义务教育均衡发展,其中某项“改薄工程”建设,甲队单独完成需要20天,若由甲队先做13天,则剩下的工程由甲、乙两队合作3天完成.问乙队单独完成这项工程需要多少天?若设乙队单独完成这项工程需要x天,根据题意可列方程为( )
| A. | 13+3+x=20 | B. | $\frac{13}{20}$+3($\frac{1}{20}$+$\frac{1}{x}$)=1 | C. | $\frac{13}{20}$+$\frac{3}{x}$=1 | D. | (1-$\frac{13}{20}$)+x=3 |
16.-8的立方根是( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |
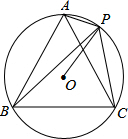 如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( )
如图,点P是等边三角形ABC外接圆⊙O上的点(点P与点A、B、C不重合),有下列结论:①当弦PB最长时,PA=PC;②当∠ACP=30°时,弦PB最长;③当PO⊥AB时,∠ACP=30°;④当△APC是等腰三角形时,PO⊥AC,其中正确结论的个数是( )