题目内容
6.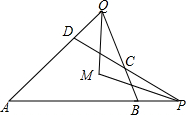 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.(1)若∠ADC=∠ABC=90°,求证:PM⊥QM;
(2)若∠A+∠DCB=180°,则PM⊥QM还成立啊?请说明理由.
分析 (1)连接PQ,由∠ADC=∠ABC=90°,于是得到∠PDQ=∠QBP=90°,根据PM,QM分别平分∠APC和∠AQC,于是得到∠1=∠2=∠4,由于∠1+∠2+∠3+∠4=90°,推出∠2+∠3+∠4+∠5=90°,即可得到结论;
(2)PM⊥QM,根据PM,QM分别平分∠APC和∠AQC,得到∠APC=2∠4,∠AQC=2∠2,根据三角形的内角和得到∠A+2∠2+2∠4+∠3+∠5=∠QCP+∠3+∠5=180°,由已知条件∠3+∠5+2∠2+2∠4+∠3+∠5=180°,于是得到∠3+∠2+∠4+∠5=90°,于是得到结论.
解答  解:(1)连接PQ,
解:(1)连接PQ,
∵∠ADC=∠ABC=90°,
∴∠PDQ=∠QBP=90°,∵∠DCQ=∠BCP,
∴∠DQC=∠BPC,
∵PM,QM分别平分∠APC和∠AQC,
∴∠1=∠2=∠4,
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3+∠4+∠5=90°,
∴∠M=90°,
∴PM⊥QM;
(2)PM⊥QM,
理由:∵PM,QM分别平分∠APC和∠AQC,
∴∠APC=2∠4,∠AQC=2∠2,
∵∠A+2∠2+2∠4+∠3+∠5=∠QCP+∠3+∠5=180°,
∵∠A+∠BCD=180°,∠BCD=∠PCQ,
∴∠A=∠3+∠5,
∴∠3+∠5+2∠2+2∠4+∠3+∠5=180°,
∴∠3+∠2+∠4+∠5=90°,
∴∠M=90°,
∴PM⊥QM.
点评 本题考查了三角形的内角和,角平分线的定义,垂直的定义,正确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
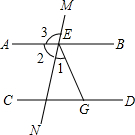 如图,AB∥CD,∠1:∠2:∠3=1:4:5
如图,AB∥CD,∠1:∠2:∠3=1:4:5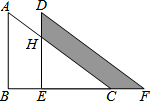 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移BE的距离,就得到此图形,其中AB=10cm,BE=6cm,DH=4cm,求阴影部分的面积.
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移BE的距离,就得到此图形,其中AB=10cm,BE=6cm,DH=4cm,求阴影部分的面积. 已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.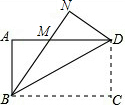 如图,把一张矩形的纸沿对角线折叠,若AB=4cm,BM=5cm,则△BMD的面积S=10cm2.
如图,把一张矩形的纸沿对角线折叠,若AB=4cm,BM=5cm,则△BMD的面积S=10cm2.