题目内容
1.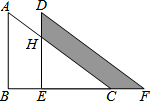 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移BE的距离,就得到此图形,其中AB=10cm,BE=6cm,DH=4cm,求阴影部分的面积.
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移BE的距离,就得到此图形,其中AB=10cm,BE=6cm,DH=4cm,求阴影部分的面积.
分析 根据平移的性质有:DE=AB;BE=CF;CH∥DF.根据已知可求EH;由平行线分线段成比例定理可求EC.从而可计算△EFD和△ECH的面积.阴影部分面积等于二者之差.
解答 解:方法1,根据题意得,DE=AB=10cm,BE=CF=6cm,CH∥DF.
∴EH=10-4=6cm,
EH:HD=EC:CF,即 6:4=EC:6,
∴EC=9.
∴S△EFD=$\frac{1}{2}$×10×(9+6)=75;
S△ECH=$\frac{1}{2}$×6×9=27.
∴S阴影部分=75-27=48(cm2).
方法2,根据题意得,DE=AB=10cm,BE=CF=6cm,CH∥DF.
∴EH=10-4=6cm,
∴S阴影=S梯形ABEH=$\frac{1}{2}$(10+6)×6=48;
故答案为 48.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.本题关键要找到平移的对应点.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为1:2:3 | B. | 三边平方的比为1:2:3 | ||
| C. | 三边长为41,40,9 | D. | 三边长为10,15,20 |
16.甲、乙两班举行电脑汉字录入比赛,成绩如下:
要从甲、乙两班选一个班的部分学生外出参加比赛,应选哪个班?
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| 甲 | 55 | 119 | 191 | 115 |
| 乙 | 55 | 121 | 110 | 115 |
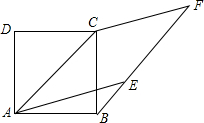 如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.
如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.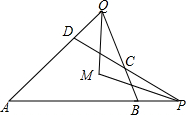 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.