题目内容
18. 已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
已知点A(-4,a),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)求一次函数与反比例函数的解析式;
(2)根据图象,直接写出不等式kx+b>$\frac{m}{x}$的解集;
(3)P是线段AB上的一点,连接PC,PD,若S△PAC=2S△PBD,求点P坐标.
分析 (1)先利用待定系数法求反比例函数解析式,然后把点A(-4,a)代入可计算出a的值,然后把A、B的坐标代入一次函数y=kx+b,利用待定系数法即可求得一次函数的解析式;
(2)观察函数图象得到当-4<x<-1时,一次函数图象都在反比例函数图象上方;
(3)设P点坐标为(t,$\frac{1}{2}$t+$\frac{5}{2}$),利用三角形面积公式可得到$\frac{1}{2}$×$\frac{1}{2}$(t+4)=2×$\frac{1}{2}$×1×(2-$\frac{1}{2}$t-$\frac{5}{2}$),解方程得到t=-2,从而可确定P点坐标.
解答 解:(1)把B(-1,2)代入y=$\frac{m}{x}$(m≠0,x<0)得,2=$\frac{m}{-1}$,
解得m=-2,
所以反比例函数的解析式为y=-$\frac{2}{x}$(m≠0,x<0);
把A(-4,a)代入y=-$\frac{2}{x}$(m≠0,x<0)得,a=-$\frac{2}{-4}$=$\frac{1}{2}$,
把A(-4,$\frac{1}{2}$),B(-1,2)代入y=kx+b得,
$\left\{\begin{array}{l}{-4k+b=\frac{1}{2}}\\{-k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴所以一次函数解析式为y=$\frac{1}{2}$x+$\frac{5}{2}$;
(2)不等式kx+b>$\frac{m}{x}$的解集当为-4<x<-1;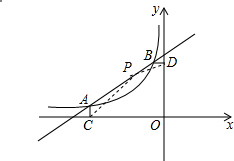
(3)连接PC、PD,如图,
设P点坐标为(t,$\frac{1}{2}$t+$\frac{5}{2}$).
∵S△PAC=2S△PBD,
∴$\frac{1}{2}$×$\frac{1}{2}$(t+4)=2×$\frac{1}{2}$×1×(2-$\frac{1}{2}$t-$\frac{5}{2}$),
解得t=-2,
∴P点坐标为(-2,$\frac{3}{2}$).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
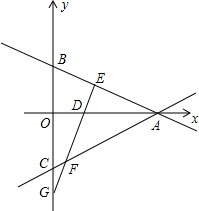 如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB.
如图,在平面直角坐标系中,一直线分别与坐标轴交于A(a,0)、B(0,b)两点,满足$\sqrt{(a-3)^{2}}$+|b-1|=0,在y轴负半轴上截取OC=OB.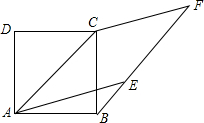 如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.
如图,正方形ABCD中,AB=$\sqrt{2}$,点F为正方形ABCD外一点,点E在BF上,且四边形AEFC是菱形.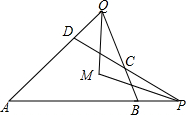 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.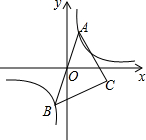 如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.
如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.