题目内容
12.一次函数y=-x+1与反比例函数y=$\frac{k}{x}$(k<0)中,x与y的部分对应值如表:| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=-x+1 | 4 | 3 | 2 | 0 | -1 | -2 |
| y=$\frac{k}{x}$ | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ |
分析 先利用表中的对应值确定一次函数y=-x+1与反比例函数y=$\frac{k}{x}$(k<0)图象的交点坐标,然后利用函数图象,写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可.
解答 解:由表中的对应值可得一次函数y=-x+1与反比例函数y=$\frac{k}{x}$(k<0)图象的交点坐标为(-1,2)和(2,-1),
所以当-1<x<0或x>2时,$\frac{k}{x}$>-x+1,
即不等式$\frac{k}{x}$+x-1>0的解集为-1<x<0或x>2
故答案为-1<x<0或x>2
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14. 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
根据以上信息,解答下列问题.
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.
 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表. | 投中篮的次数(次) | 频数 (人数) | 频率 |
| 0 | 2 | 0.05 |
| 1 | 12 | 0.3 |
| 2 | x | 0.45 |
| 3 | 8 | y |
| 合计 | m | 1 |
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.
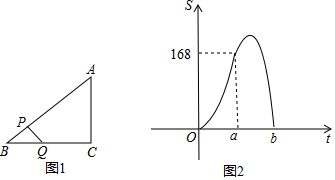
17.点P在∠AOB的平分线上,点P到OA边的距离等于9,点Q是OB边上的任意一点,则下列选项正确的是( )
| A. | PQ≥9 | B. | PQ>9 | C. | PQ<9 | D. | PQ≤9 |
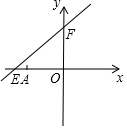 如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
如图,直线y=kx+6与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).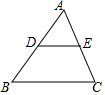 如图,在△ABC中,DE∥BC,AD=DB,那么DE:BC=1:2.
如图,在△ABC中,DE∥BC,AD=DB,那么DE:BC=1:2.