题目内容
2.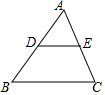 如图,在△ABC中,DE∥BC,AD=DB,那么DE:BC=1:2.
如图,在△ABC中,DE∥BC,AD=DB,那么DE:BC=1:2.
分析 由条件可证得DE为△ABC的中位线,则可求得答案.
解答 解:
∵DE∥BC,AD=DB,
∴$\frac{AE}{EC}$=$\frac{AD}{DB}$=1,
∴E为AC的中点,
∴DE为△ABC的中位线,
∴DE:BC=1:2,
故答案为:1:2.
点评 本题主要考查三角形中位线定理,证得DE为△ABC的中位线是解题的关键.

练习册系列答案
相关题目
12.一次函数y=-x+1与反比例函数y=$\frac{k}{x}$(k<0)中,x与y的部分对应值如表:
则不等式$\frac{k}{x}$+x-1>0的解集为-1<x<0或x>2.
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=-x+1 | 4 | 3 | 2 | 0 | -1 | -2 |
| y=$\frac{k}{x}$ | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ |
10.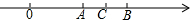 如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )
如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )
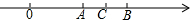 如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )
如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )| A. | 2-$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $\sqrt{5}$-2 |
12.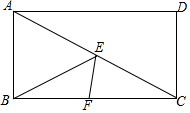 如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
 如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )
如图,在矩形ABCD中,AB=2,BC=4,点E和点F分别是AC和BC上的动点,在点E和点F运动的过程中,BE+EF的最小值为( )| A. | $\frac{16}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
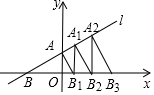 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为$(\frac{4}{3})^{n}\sqrt{3}-\sqrt{3}$.