题目内容
17．点P在∠AOB的平分线上，点P到OA边的距离等于9，点Q是OB边上的任意一点，则下列选项正确的是（ ）| A． | PQ≥9 | B． | PQ＞9 | C． | PQ＜9 | D． | PQ≤9 |
分析 根据角平分线上的点到角的两边距离相等可得点P到OB的距离为9，再根据垂线段最短解答．
解答 解：∵点P在∠AOB的平分线上，点P到OA边的距离等于9，
∴点P到OB的距离为9，
∵点Q是OB边上的任意一点，
∴PQ≥9．
故选A．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短的性质，熟记性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
19．
如图，A（0，-$\sqrt{2}$），点B为直线y=-x上一动点，当线段AB最短时，点B的坐标为（ ）
如图，A（0，-$\sqrt{2}$），点B为直线y=-x上一动点，当线段AB最短时，点B的坐标为（ ）| A． | （0，0） | B． | （1，-1） | C． | （$\frac{1}{2}$，-$\frac{1}{2}$） | D． | （$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$） |
“龟兔赛跑”的故事同学们都非常熟悉，图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，下列说法：
12．一次函数y=-x+1与反比例函数y=$\frac{k}{x}$（k＜0）中，x与y的部分对应值如表：
则不等式$\frac{k}{x}$+x-1＞0的解集为-1＜x＜0或x＞2．
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=-x+1 | 4 | 3 | 2 | 0 | -1 | -2 |
| y=$\frac{k}{x}$ | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ |
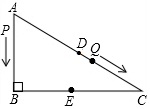如图，在Rt△ABC中，∠B=90°，∠C=30°，AB=12厘米，点P从A出发沿线路AB-BC作匀速运动，点Q从AC的中点D同时出发沿线路DC-CB作匀速运动逐步靠近点P．设两点P、Q的速度分别为1厘米/秒、a厘米/秒（a＞1），它们在t秒后于BC边上的某一点E相遇． 
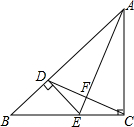已知，如图，△ABC中，AC=BC，∠C=90°，AE平分∠BAC交BC于E，过E作ED⊥AB于D，连接DC交AE于F，其中BD=1，下列结论：①DC⊥AE；②AB=2+$\sqrt{2}$；③CD•AE=2$\sqrt{2}$+2；④$\frac{AE}{CD}$=2：1，其中正确的结论是①②③．