题目内容
14.若(|a-3|-1)0+(2a-1)-4有意义,则a的取值范围是a≠2且a≠4且a≠$\frac{1}{2}$.分析 根据零指数幂有意义的条件,负整数指数幂有意义的条件,可得|a-3|-1≠0且2a-1≠0,依此即可求解.
解答 解:∵(|a-3|-1)0+(2a-1)-4有意义,
∴|a-3|-1≠0且2a-1≠0,
解得a≠2且a≠4且a≠$\frac{1}{2}$.
故答案为:a≠2且a≠4且a≠$\frac{1}{2}$.
点评 考查了负整数指数幂,零指数幂,关键是根据题意得到|a-3|-1≠0且2a-1≠0.

练习册系列答案
相关题目
5.观察下列图形请您从图①、图②、图③中找出规律,按照相同规律求出图④中的数y和图⑤中的数x,那么x+y的值为( )


| A. | 10 | B. | -14 | C. | -12 | D. | 6 |
2.函数y=$\frac{x}{\sqrt{x+3}}$中自变量x的取值范围是( )
| A. | x>-3且x≠0 | B. | x≠0 | C. | x>-3 | D. | x≠-3或x≠0 |
9.若x=1是关于x的一元一次方程ax-b-2=0(a≠0)的一个根,则a-b的值等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | 3 |
6.在△ABC中,$(\sqrt{3}tanA-3{)^2}+|2cosB-\sqrt{3}|=0$,则△ABC为( )
| A. | 直角三角形 | B. | 等边三角形 | ||
| C. | 含60°的任意三角形 | D. | 是顶角为钝角的等腰三角形 |
3. 如下图,下列条件中,能判断直线l1∥l2的是( )
如下图,下列条件中,能判断直线l1∥l2的是( )
 如下图,下列条件中,能判断直线l1∥l2的是( )
如下图,下列条件中,能判断直线l1∥l2的是( )| A. | ∠2=∠3 | B. | ∠4+∠5=180° | C. | ∠1=∠3 | D. | ∠2=∠4 |
4.下列方程中是二元一次方程的是( )
| A. | $\frac{2y-1}{5}=2-\frac{3x-2}{4}$ | B. | x2-4y=5 | C. | x-y=x+y | D. | $\frac{y+1}{x}=3$ |
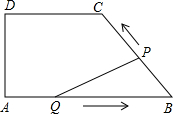 如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题: