题目内容
6．在△ABC中，$（\sqrt{3}tanA-3{）^2}+|2cosB-\sqrt{3}|=0$，则△ABC为（ ）| A． | 直角三角形 | B． | 等边三角形 | ||
| C． | 含60°的任意三角形 | D． | 是顶角为钝角的等腰三角形 |
分析 首先结合绝对值以及偶次方的性质得出$\sqrt{3}$tanA-3=0，2cosB-$\sqrt{3}$=0，进而利用特殊角的三角函数值得出答案．
解答 解：∵（$\sqrt{3}$tanA-3）2+|2cosB-$\sqrt{3}$|=0，
∴$\sqrt{3}$tanA-3=0，2cosB-$\sqrt{3}$=0，
∴tanA=$\sqrt{3}$，cosB=$\frac{\sqrt{3}}{2}$，
∠A=60°，∠B=30°，
∴△ABC为直角三角形．
故选：A．
点评 此题主要考查了绝对值以及偶次方的性质和特殊角的三角函数值等知识，熟练记忆特殊角的三角函数值是解题关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
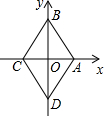菱形ABCD在直角坐标系中的位置如图所示，其中点A的坐标为（1，0），点B的坐标为（0，$\sqrt{3}$），动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，移动到第2015秒时，点P的坐标为（$\frac{3}{4}$，-$\frac{\sqrt{3}}{4}$）．
17．甲比乙大15岁，5年前甲的年龄是乙的年龄的2倍，则乙现在的年龄是（ ）
| A． | 10岁 | B． | 15岁 | C． | 20岁 | D． | 30岁 |