题目内容
1. 如图,直线m的表达式为y=-3x+3,且与x轴交于点B,直线n经过点A(4,0),且与直线m交于点C(t,-3)
如图,直线m的表达式为y=-3x+3,且与x轴交于点B,直线n经过点A(4,0),且与直线m交于点C(t,-3)(1)求直线n的表达式.
(2)求△ABC的面积.
(3)在直线n上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标.
分析 (1)把C点坐标代入直线m,可求得t,再由待定系数法可求得直线n的解析式;
(2)可先求得B点坐标,则可求得AB,再由C点坐标可求得△ABC的面积;
(3)由面积相等可知点P到x轴的距离和点C到y轴的距离相等,可求得P点纵坐标,代入直线n的解析式可求得P点坐标.
解答 解:(1)∵直线m过C点,
∴-3=-3t+3,解得t=2,
∴C(2,-3),
设直线n的解析式为y=kx+b,
把A、C两点坐标代入可得$\left\{\begin{array}{l}{4k+b=0}\\{2k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1.5}\\{b=-6}\end{array}\right.$,
∴直线n的解析式为y=1.5x-6;
(2)在y=-3x+3中,令y=0,可得0=-3x+3,解得x=1,
∴B(1,0),且A(4,0),
∴AB=4-1=3,且C点到x轴的距离h=3,
∴S△ABC=$\frac{1}{2}$AB•h=$\frac{1}{2}$×3×3=4.5;
(3)由点P在直线n上,故可设P点坐标为(x,1.5x-6),
∵S△ABC=S△ABP,
∴P到x轴的距离=3,
∵C、P两点不重合,
∴P点的纵坐标为3,
∴1.5x-6=3,解得x=6,
∴P点坐标为(6,3).
点评 本题主要考查直线的交点问题,掌握两直线的交点坐标满足每条直线的解析式是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
12.直角三角形的两条直角边长为3和4,则该直角三角形斜边上的高为( )
| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | $\frac{24}{5}$ |
16.下列图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 菱形 | B. | 平行四边形 | C. | 等边三角形 | D. | 梯形 |
6.已知直角坐标系中点P到x轴的距离为3,到y轴的距离为5,则满足条件的点P的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.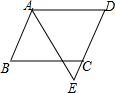 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 2.5 |