题目内容
11.解不等式组$\left\{\begin{array}{l}{2(x+2)≤3x+3}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$,并将不等式组的解集在数轴上表示出来.分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:由2(x+2)≤3x+3,可得:x≥1,
由$\frac{x}{3}$<$\frac{x+1}{4}$,可得:x<3,
则不等式组的解为:1≤x<3,
不等式组的解集在数轴上表示如图所示:
点评 本题考查了一元一次不等式组,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
1.在下列长度的四组线段中,不能组成直角三角形的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 1,1,$\sqrt{2}$ | D. | 4,5,6 |
3.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列关于方程x2+x-1=0的说法中正确的是( )
| A. | 该方程有两个相等的实数根 | |
| B. | 该方程有两个不相等的实数根,且它们互为相反数 | |
| C. | 该方程有一根为$\frac{{1+\sqrt{5}}}{2}$ | |
| D. | 该方程有一根恰为黄金比例 |
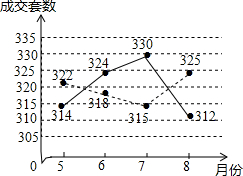 当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).
当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据). 如图,用三个大写字母表示∠1为∠MCB;∠2为∠AMC;∠3为∠CAN.
如图,用三个大写字母表示∠1为∠MCB;∠2为∠AMC;∠3为∠CAN.