题目内容
4. 如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由.
如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由.
分析 先根据勾股定理计算BD的长,再利用勾股定理的逆定理证明∠DBC=90°,所以:△BCD是直角三角形.
解答 解:△BCD是直角三角形,理由是:
在△ABD中,∠A=90°,
∴BD2=AD2+AB2=32+42=25,
在△BCD中,BD2+BC2=52+122=169,
CD2=132=169,
∴BD2+BC2=CD2,
∴∠DBC=90°
∴△BCD是直角三角形.
点评 本题考查了勾股定理及其逆定理,熟练掌握定理的内容是关键,注意各自的条件和结论.

练习册系列答案
相关题目
6.欧拉公式中,多面体的面数F,棱数E,顶点数V之间的正确关系是( )
| A. | F+V-E=2 | B. | F+E-V=2 | C. | E+V-F=2 | D. | E-V-F=2 |
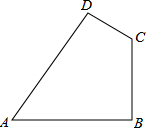 如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
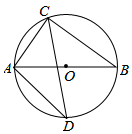 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.