题目内容
9. 在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )
在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )| A. | 70° | B. | 75° | C. | 105° | D. | 110° |
分析 首先利用等腰三角形的性质求得∠DAC的度数,然后求得∠BDA的度数,最后利用等腰三角形的性质求得∠B的度数.
解答 解:∵AD=DC,
∴∠DAC=∠C,
∵∠C=35°,
∴∠DAC=35°,
∴∠BDA=∠C+∠DAC═70°,
∵AB=AD,
∴∠BDA=∠B=70°.
故选:A.
点评 本题考查了等腰三角形的性质:等腰三角形两底角相等.

练习册系列答案
相关题目
17.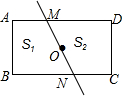 如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
 如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )| A. | S1<S2 | B. | S1>S2 | ||
| C. | S1=S2 | D. | S1与S2的关系由直线的位置而定 |
14.抛物线y=3x2,y=-3x2,y=-3x2+3共有的性质是( )
| A. | 开口向上 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x值的增大而增大 |
18.如果等腰三角形有一条边长是6,另一条边长是8,那么它的周长是( )
| A. | 20 | B. | 20或22 | C. | 22 | D. | 24 |
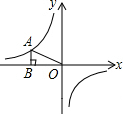 如图,过反比例函数y=$\frac{k}{x}$的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为-6.
如图,过反比例函数y=$\frac{k}{x}$的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为-6. 如图,在△ABC中,点D是BC的中点,点G为△ABC的重心,AG=2,则DG=1.
如图,在△ABC中,点D是BC的中点,点G为△ABC的重心,AG=2,则DG=1.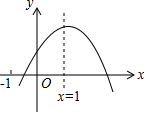 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2,其中正确的结论是②④.(填入正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2,其中正确的结论是②④.(填入正确结论的序号)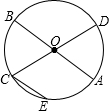 如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.
如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.