题目内容
1.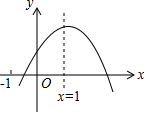 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2,其中正确的结论是②④.(填入正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a-b+c>0,④4a+2b+c>0,⑤若点(-2,y1)和(-$\frac{1}{3}$,y2)在该图象上,则y1>y2,其中正确的结论是②④.(填入正确结论的序号)
分析 根据二次函数的图象与性质即可判断.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∵对称轴x=-$\frac{b}{2a}$>0,
∴b>0,
∴abc<0,故①正确;
∵对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a,
∴令x=-1时,此时y=a-b+c,
由图象可知a-b+c<0,
∴a+2a+c=3a+c<0,故②正确,③错误;
∵抛物线的对称轴为x=1,
∴-1与3关于x=1对称,0与2关于x=1对称,
令x=2时,此时y=4a+2b+c>0,故④正确;
当x<1时,y随着x的增大而增大,
∴-2<-$\frac{1}{3}$,
∴y1<y2,故⑤错误;
故答案为:②④
点评 本题考查二次函数的图象与性质,涉及抛物线的对称轴,开口方向,抛物线与x轴交点个数等知识,较为综合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.3的相反数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
9. 在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )
在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )
 在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )
在△ABC中,AB=AD=DC,∠C=35°,则∠B的度数为( )| A. | 70° | B. | 75° | C. | 105° | D. | 110° |
10.下列说法中正确的是( )
| A. | 0既不是整数也不是分数 | B. | 整数和分数统称有理数 | ||
| C. | 一个数的绝对值一定是正数 | D. | 绝对值等于本身的数是0和1 |
11. 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
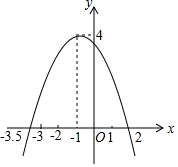 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0)和(-3.5,0),顶点为(-1,4),根据图象直接写出下列答案.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0)和(-3.5,0),顶点为(-1,4),根据图象直接写出下列答案. 有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,c2=4.试求:$\frac{a}{b}$+$\frac{a+b}{2017{c}^{2}}$-3(a+b+c)的值.
有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,c2=4.试求:$\frac{a}{b}$+$\frac{a+b}{2017{c}^{2}}$-3(a+b+c)的值.