题目内容
17．
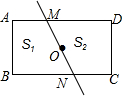如图，经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分，则S1与S2的大小关系是（ ）| A． | S1＜S2 | B． | S1＞S2 | ||
| C． | S1=S2 | D． | S1与S2的关系由直线的位置而定 |
分析 根据矩形对角线相等且平分的性质，易证△AOB≌△COD（SSS），△OMD≌△ONB，△AMO≌△CNO，即可证明S1=S2，即可解题．
解答 
解：矩形ABCD中，AD=BC，
AO=BO=CO=DO，
∴△AOB≌△COD（SSS），
∵∠MDO=∠OBN，OB=OD，∠MOD=∠NOB，
∴△OMD≌△ONB，
同理可证，△AMO≌△CNO，
∴S1=S2．
故选C．
点评 本题考查了矩形对角线相等且互相平分的性质，全等三角形的证明，全等三角形面积相等的性质，本题中求证三角形全等是解题的关键．
练习册系列答案
相关题目
7．已知⊙O的半径为5．若OP=6，则点P与⊙O的位置关系是（ ）
| A． | 点P在⊙O内 | B． | 点P在⊙O上 | C． | 点P在⊙O外 | D． | 无法判断 |
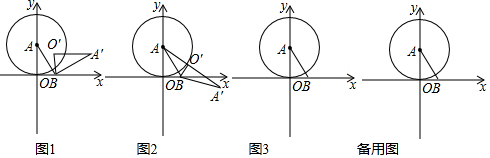
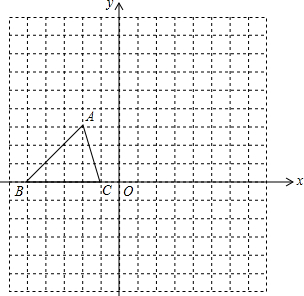如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）．
9．
在△ABC中，AB=AD=DC，∠C=35°，则∠B的度数为（ ）
在△ABC中，AB=AD=DC，∠C=35°，则∠B的度数为（ ）| A． | 70° | B． | 75° | C． | 105° | D． | 110° |