题目内容
19．
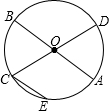如图，已知AB和CD是⊙O的两条直径，CE∥AB，若$\widehat{CE}$的度数为40°，则$\widehat{AE}$的度数为70°．
分析 接OE，根据$\widehat{CE}$的度数为40°求出∠COE的度数，再由等腰三角形的性质求出∠E的度数，根据平行线的性质即可得出结论．
解答 
解：连接OE，
∵$\widehat{CE}$=40°，
∴∠COE=40°．
∵OC=OE，
∴∠E=$\frac{180°-40°}{2}$=70°．
∵CE∥AB，
∴∠AOE=∠E=70°，
∴$\widehat{AE}$的度数为70°，
故答案为：70°．
点评 本题考查的是圆心角、弧、弦的关系及平行线的性质，等腰三角形的性质及三角形内角和定理，比较简单．
练习册系列答案
相关题目
9．
在△ABC中，AB=AD=DC，∠C=35°，则∠B的度数为（ ）
在△ABC中，AB=AD=DC，∠C=35°，则∠B的度数为（ ）| A． | 70° | B． | 75° | C． | 105° | D． | 110° |
10．下列说法中正确的是（ ）
| A． | 0既不是整数也不是分数 | B． | 整数和分数统称有理数 | ||
| C． | 一个数的绝对值一定是正数 | D． | 绝对值等于本身的数是0和1 |
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①abc＜0；②b2-4ac＞0；③m＞2；④当x＜0时，y随x的增大而增大．其中正确结论的个数是（ ）
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，则在数轴上A、B两点之间的距离AB=|a-b|．
11．
有理数a、b、c在数轴上的位置如图所示，化简|a-b|+|c-a|-|b-c|的结果是（ ）
有理数a、b、c在数轴上的位置如图所示，化简|a-b|+|c-a|-|b-c|的结果是（ ）| A． | -2a | B． | -2b | C． | -2a-2b | D． | 2a-2b |
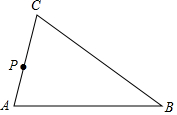如图，在△ABC中，点P为AC上一点，请利用尺规在BC边上求作一点Q，使得△ABC∽△QPC（保留作图痕迹，不写作法）