题目内容
18.在平面直角坐标系中,A为反比例函数y=$\frac{m}{x}(m<0)$图象上的一点,若点A到x轴的距离是2,到y轴的距离是3,解关于x的不等式$\frac{2x}{m}-5≥2-\frac{mx}{3}$,并将其解集在数轴上表示出来.分析 根据题意知m的值,还原不等式,解不等式可得解集,并表示在数轴上.
解答 解:由题意可知点m=-6,
∴关于x的不等式为-$\frac{x}{3}$-5≥2+2x,
解得:x≤-3,
解集在数轴上的表示如图:
点评 本题主要考查反比例函数图象上点的坐标的特点及解不等式的能力,根据反比例系数是图象上任意一点横、纵坐标乘积是解不等式的前提,解不等式是本题考查的根本.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列方程是一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-2x=x2+1 | C. | 4x2-9=(2x-1)2 | D. | x2-1=0 |
6.计算-(-1)2014的结果是( )
| A. | 2014 | B. | -2014 | C. | 1 | D. | -1 |
13.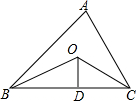 如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
 如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
3.如图,将一长方形纸条沿EF折叠,若∠AFD=50°,则∠CEB等于( )


| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
10.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
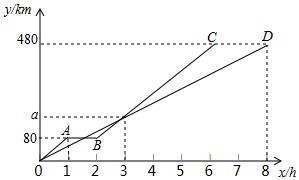 甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.