题目内容
8.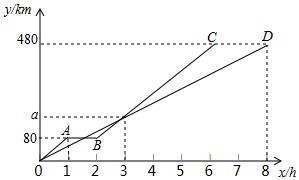 甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.(1)求a的值;
(2)求两车第一次相遇的时间;
(3)两车出发多长时间,货车在客车前面20km?
分析 (1)由函数图象,可知货车8小时行驶了480千米,从而可以求得货车的速度,然后用货车的速度乘以3小时,即可求得a的值;
(2)由函数图象可知两车第一次相遇在客车检修时,从而令货车的路程等于80即可求得货车用的时间,本题得以解决;
(3)根据题意可知货车在客车前20km有两种情况,然后分别计算即可解答本题.
解答 解:(1)由图象可得,
货车的速度为:480÷8=60(千米/h),
当x=3时,a=60×3=180千米,
即a的值是180千米;
(2)由图象可知,点B的坐标为(8,480),
设过点O、B的直线的解析式为:y=kx,
480=8k,
解得,k=60
即过点O、B的直线的解析式为:y=60x,
将y=80代入y=60x,得x=$\frac{4}{3}$,
即两车第一次相遇的时间是$\frac{4}{3}$小时;
(3)当1<x<2时,
将y=100代入y=60x,得x=$\frac{5}{3}$,
由图象可得,点B的坐标为(2,80),点C的坐标为(6,480),
设过点B、C的直线的解析式为:y=kx+b,
$\left\{\begin{array}{l}{2k+b=80}\\{6k+b=480}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=100}\\{b=-120}\end{array}\right.$
即过点B、C的直线的解析式为:y=100x-120,
∴60x-(100x-120)=20,得x=2.5
即两车出发的时间为$\frac{5}{3}$小时或2.5小时时,货车在客车前面20km.
点评 本题考查一次函数的应用、求函数的解析式,解题的关键是明确题意,找出所求问题需要的条件,认真计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列判断不正确的是( )
| A. | 所有等腰直角三角形都相似 | B. | 所有直角三角形都相似 | ||
| C. | 所有正六边形都相似 | D. | 所有等边三角形都相似 |
20.下列等式成立的是( )
| A. | $\frac{2}{2x+y}=\frac{1}{x+y}$ | B. | (-x-1)(1-x)=1-x2 | C. | $\frac{x}{-x+y}=-\frac{x}{x+y}$ | D. | (-x-1)2=x2+2x+1 |
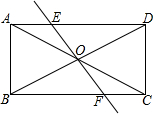 如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④.
如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④. 如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.
如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.