题目内容
3．如图，将一长方形纸条沿EF折叠，若∠AFD=50°，则∠CEB等于（ ）
| A． | 50° | B． | 60° | C． | 65° | D． | 70° |
分析 根据两直线平行，内错角相等求出∠1=∠AFD，∠CEB=∠1，即可得解．
解答 解：∵DF∥CE，∠AFD=50°，
∴∠1=∠AFD，
∵AF∥BE，
∴∠CEB=∠1，
∴∠CEB=∠AFD，
∵∠AFD=50°，
∴∠CEB=50°，
故选A．
点评 本题考查了两直线平行，内错角相等的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
相关题目
14．下列说法正确的是（ ）
| A． | 有一组邻边相等的四边形是菱形 | |
| B． | 有一个角是直角的菱形是正方形 | |
| C． | 对角线相等的四边形是矩形 | |
| D． | 一组对边平行，另一组对边相等的四边形是平行四边形 |
11．已知3a=3b-4，则代数式3a2-6ab+3b2-4的值为（ ）
| A． | $\frac{4}{3}$ | B． | -$\frac{4}{3}$ | C． | 2 | D． | 3 |
8．
为迎接市教育局开展的“学雷锋•做有道德的人”主题演讲活动，某区教育局团委组织各校学生进行演讲预赛，然后将所有参赛学生的成绩（得分为整数，满分为100分）分成四组，绘制了不完整的统计图表如下：
观察图表信息，回答下列问题：
（1）参考学生共有25人；
（2）如果将各组的组中值视为该组的平均成绩，请你估算所有参赛学生的平均成绩；
（3）小娟说：“根据以上统计图表，我可以确定所有参赛学生成绩的中位数在哪一组，但不能确定众数在哪一组？”你同一她的观点么？请说明理由．
（4）成绩落在第一组的恰好是两男两女四位学生，区团委从中随机挑选两位学生参加市教育局组织的决赛，通过列表或画树状图求出挑选的两位学生恰好是一男一女的概率．
为迎接市教育局开展的“学雷锋•做有道德的人”主题演讲活动，某区教育局团委组织各校学生进行演讲预赛，然后将所有参赛学生的成绩（得分为整数，满分为100分）分成四组，绘制了不完整的统计图表如下：| 组别 | 成绩x | 组中值 | 频数 |
| 第一组 | 90≤x≤100 | 95 | 4 |
| 第二组 | 80≤x＜90 | 85 | 10 |
| 第三组 | 70≤x＜80 | 75 | 8 |
| 第四组 | 60≤x＜70 | 65 | 3 |
（1）参考学生共有25人；
（2）如果将各组的组中值视为该组的平均成绩，请你估算所有参赛学生的平均成绩；
（3）小娟说：“根据以上统计图表，我可以确定所有参赛学生成绩的中位数在哪一组，但不能确定众数在哪一组？”你同一她的观点么？请说明理由．
（4）成绩落在第一组的恰好是两男两女四位学生，区团委从中随机挑选两位学生参加市教育局组织的决赛，通过列表或画树状图求出挑选的两位学生恰好是一男一女的概率．
15．如果OC是∠AOB的平分线，则下列结论不正确的是（ ）
| A． | ∠AOC=∠BOC | B． | 2∠AOC=∠AOB | C． | ∠AOB=2∠BOC | D． | ∠AOB=∠AOC |
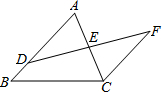如图，D是△ABC的边AB上一点，E是AC的中点，过点C作CF∥AB，交DE的延长线于点F．求证：AB=CF+BD．