题目内容
20.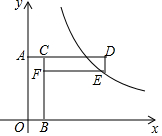 已知:如图,矩形AOBC与矩形CDEF全等,且AC=CF=1,按如图所示方式放置在平面直角坐标系中,其中点A落在y轴上,点B落在x轴上,点F落在BC上.若反比例函数y=$\frac{15}{x}$在第一象限的图象经过点E,则OA的长为4.
已知:如图,矩形AOBC与矩形CDEF全等,且AC=CF=1,按如图所示方式放置在平面直角坐标系中,其中点A落在y轴上,点B落在x轴上,点F落在BC上.若反比例函数y=$\frac{15}{x}$在第一象限的图象经过点E,则OA的长为4.
分析 设OA=x,根据矩形AOBC与矩形CDEF全等和AC=CF=1得出E点的坐标为(x+1,x-1),把E点的坐标代入y=$\frac{15}{x}$,即可求出答案.
解答 解:设OA=x,
∵矩形AOBC与矩形CDEF全等,AC=CF=1,
∴OA=BC=EF=x,AC=CF=DE=1,
∴E点的坐标为(x+1,x-1),
把E点的坐标代入y=$\frac{15}{x}$得:x-1=$\frac{15}{x+1}$,
解得:x=4或x=-4(舍去),
故答案为:4.
点评 本题考查了反比例函数图象上点的坐标特征,矩形的性质等知识点,能求出E的坐标是解此题的关键.

练习册系列答案
相关题目
10.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对巢湖水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 节能灯厂家对一批节能灯管使用寿命的调查 | |
| D. | 对某班50名学生视力情况的调查 |
8. 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )| A. | 0.6x+0.4y+100=500 | B. | 0.6x+0.4y-100=500 | ||
| C. | 0.4x+0.6y+100=500 | D. | 0.4x+0.6y-100=500 |
15.若关于x的一元二次方程x2+mx+m-4=0有一根为0,则m的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
5.估计2$\sqrt{13}$-1的值介于( )
| A. | 4和5之间 | B. | 5和6之间 | C. | 6和7之间 | D. | 7和8之间 |
12.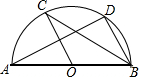 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )| A. | 10° | B. | 15° | C. | 30° | D. | 45° |
9.(-$\frac{1}{3}$)0=( )
| A. | 1 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
10.不等式x-3≤3x+1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |