题目内容
12.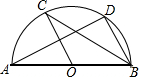 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )| A. | 10° | B. | 15° | C. | 30° | D. | 45° |
分析 首先证明OC⊥AD,推出$\widehat{AC}$=$\widehat{CD}$,推出∠CBD=∠CBA,由此即可解决问题.
解答 解: ∵AB是直径,
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BD,
∵∠A=30°,
∴∠ABD=90°-30°=60°,
∵OC∥BD,
∴OC⊥AD,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CBD=∠CBA=30°,
故选C.
点评 本题考查圆周角定理、垂径定理、直径的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
2.济宁市人口约为530060人,用科学记数法可表示为( )
| A. | 53006×10人 | B. | 0.53×106人 | C. | 5.3006×105人 | D. | 53×104人 |
7.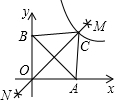 如图,点A、B的坐标分别为(2,0)、(0,2),分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交函数y=$\frac{k}{x}$(k>4)的图象于点C,则△ABC的面积为( )
如图,点A、B的坐标分别为(2,0)、(0,2),分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交函数y=$\frac{k}{x}$(k>4)的图象于点C,则△ABC的面积为( )
 如图,点A、B的坐标分别为(2,0)、(0,2),分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交函数y=$\frac{k}{x}$(k>4)的图象于点C,则△ABC的面积为( )
如图,点A、B的坐标分别为(2,0)、(0,2),分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交函数y=$\frac{k}{x}$(k>4)的图象于点C,则△ABC的面积为( )| A. | k | B. | $\sqrt{k}$ | C. | k-2 | D. | 2$\sqrt{k}$-2 |
4.若(2x+3y-12)2+|x-2y+1|=0,则xy=( )
| A. | 9 | B. | 12 | C. | 27 | D. | 64 |
1.下列图形中的曲线不表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
2.若a2-ab=0(b≠0),则$\frac{a}{a+b}$=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 0或$\frac{1}{2}$ | D. | 1或 2 |
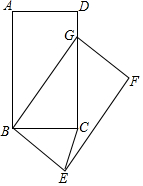 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.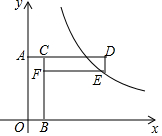 已知:如图,矩形AOBC与矩形CDEF全等,且AC=CF=1,按如图所示方式放置在平面直角坐标系中,其中点A落在y轴上,点B落在x轴上,点F落在BC上.若反比例函数y=$\frac{15}{x}$在第一象限的图象经过点E,则OA的长为4.
已知:如图,矩形AOBC与矩形CDEF全等,且AC=CF=1,按如图所示方式放置在平面直角坐标系中,其中点A落在y轴上,点B落在x轴上,点F落在BC上.若反比例函数y=$\frac{15}{x}$在第一象限的图象经过点E,则OA的长为4.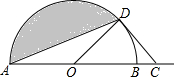 如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.
如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.