题目内容
13.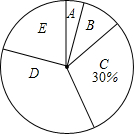 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:(1)求全班学生人数和m的值.
(2)直接学出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
分析 (1)利用C分数段所占比例以及其频数求出总数即可,进而得出m的值;
(2)利用中位数的定义得出中位数的位置;
(3)利用列表或画树状图列举出所有的可能,再根据概率公式计算即可得解.
解答 解:(1)由题意可得:全班学生人数:15÷30%=50(人);
m=50-2-5-15-10=18(人);
(2)∵全班学生人数:50人,
∴第25和第26个数据的平均数是中位数,
∴中位数落在51-56分数段;
(3)如图所示:
将男生分别标记为A1,A2,女生标记为B1
| A1 | A2 | B1 | |
| A1 | (A1,A2) | (A1,B1) | |
| A2 | (A2,A1) | (A2,B1) | |
| B1 | (B1,A1) | (B1,A2) |
点评 此题主要考查了列表法求概率以及扇形统计图的应用,根据题意利用列表法得出所有情况是解题关键.

练习册系列答案
相关题目
1.不等式2x-3<1的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
10.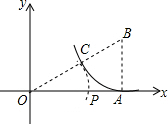 如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
 如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{3}-1$ |
8. 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
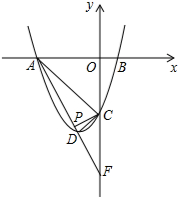 如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点,且横坐标为-2.
如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点,且横坐标为-2.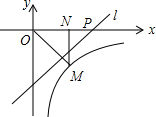 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$. 如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.
如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.