题目内容
1．不等式2x-3＜1的解集在数轴上表示为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 先解不等式得到x＜2，用数轴表示时，不等式的解集在2的左边且不含2，于是可判断D选项正确．
解答 解：2x＜4，
解得x＜2，
用数轴表示为：
．
故选D．
点评 本题考查了在数轴上表示不等式的解集：用数轴表示不等式的解集时，要注意“两定”：一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心；二是定方向，定方向的原则是：“小于向左，大于向右”．
练习册系列答案
名师指导一卷通系列答案
相关题目
11．口袋里有红、蓝、绿的三种颜色小球，6个红球，5个绿球，若任意摸出一个绿球的概率是0.25，则任意摸出篮球的概率是多少？（ ）
| A． | 0.25 | B． | 0.4 | C． | 0.45 | D． | 0.5 |
12．
如图，AB∥CD，EF平分∠AEG，若∠FGE=40°，那么∠EFG的度数为（ ）
如图，AB∥CD，EF平分∠AEG，若∠FGE=40°，那么∠EFG的度数为（ ）| A． | 35° | B． | 40° | C． | 70° | D． | 140° |
9．比-2015小1的数是（ ）
| A． | -2014 | B． | 2014 | C． | -2016 | D． | 2016 |
16．（1）抛物线m1：y1=a1x2+b1x+c1中，函数y1与自变量x之间的部分对应值如表：
设抛物线m1的顶点为P，与y轴的交点为C，则点P的坐标为（1，4），点C的坐标为（0，3）．
（2）将设抛物线m1沿x轴翻折，得到抛物线m2：y2=a2x2+b2x+c2，则当x=-3时，y2=12．
（3）在（1）的条件下，将抛物线m1沿水平方向平移，得到抛物线m3．设抛物线m1与x轴交于A，B两点（点A在点B的左侧），抛物线m3与x轴交于M，N两点（点M在点N的左侧）．过点C作平行于x轴的直线，交抛物线m3于点K．问：是否存在以A，C，K，M为顶点的四边形是菱形的情形？若存在，请求出点K的坐标；若不存在，请说明理由．
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
（2）将设抛物线m1沿x轴翻折，得到抛物线m2：y2=a2x2+b2x+c2，则当x=-3时，y2=12．
（3）在（1）的条件下，将抛物线m1沿水平方向平移，得到抛物线m3．设抛物线m1与x轴交于A，B两点（点A在点B的左侧），抛物线m3与x轴交于M，N两点（点M在点N的左侧）．过点C作平行于x轴的直线，交抛物线m3于点K．问：是否存在以A，C，K，M为顶点的四边形是菱形的情形？若存在，请求出点K的坐标；若不存在，请说明理由．
6．对于两个不相等的实数a、b，我们规定符号Max{a，b}表示a、b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{x，-x}=$\frac{2x+1}{x}$的解为（ ）
| A． | 1-$\sqrt{2}$ | B． | 2-$\sqrt{2}$ | C． | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D． | 1+$\sqrt{2}$或-1 |
13．
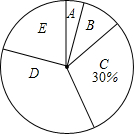今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：
（1）求全班学生人数和m的值．
（2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段．
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：（1）求全班学生人数和m的值．
（2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段．
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
| 分组 | 分数段（分） | 频数 |
| A | 36≤x＜41 | 2 |
| B | 41≤x＜46 | 5 |
| C | 46≤x＜51 | 15 |
| D | 51≤x＜56 | m |
| E | 56≤x＜61 | 10 |
15．
如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为（ ）米．
如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为（ ）米．| A． | 7tanα | B． | $\frac{7}{tanα}$ | C． | 7sinα | D． | 7cosα |
如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．