题目内容
8. 如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.
如图,点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k=$6\sqrt{3}$.
分析 首先根据点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,设A点坐标为(a,$\frac{2\sqrt{3}}{a}$),再利用含30°直角三角形的性质算出OA=2a,再利用菱形的性质进而得到B点坐标,即可求出k的值.
解答 解:因为点A在双曲线y=$\frac{{2\sqrt{3}}}{x}$(x>0)上,设A点坐标为(a,$\frac{2\sqrt{3}}{a}$),
因为四边形OABC是菱形,且∠AOC=60°,
所以OA=2a,
可得B点坐标为(3a,$\frac{2\sqrt{3}}{a}$),
可得:k=$3a×\frac{2\sqrt{3}}{a}=6\sqrt{3}$,
故答案为:$6\sqrt{3}$
点评 此题主要考查了待定系数法求反比例函数,关键是根据菱形的性质求出B点坐标,即可算出反比例函数解析式.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18. 如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )
 如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )| A. | 10 | B. | 8 | C. | 5$\sqrt{3}$ | D. | 6 |
16.(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为(1,4),点C的坐标为(0,3).
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
3.下列运算正确的是( )
| A. | 4ab÷2a=2ab | B. | (3x2)3=9x6 | C. | a3•a4=a7 | D. | $\sqrt{6}÷\sqrt{3}=2$ |
13.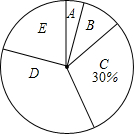 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
(1)求全班学生人数和m的值.
(2)直接学出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:(1)求全班学生人数和m的值.
(2)直接学出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
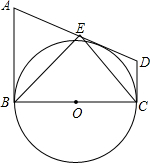 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( ) 看图找规律,“?”处应填-10.
看图找规律,“?”处应填-10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①方程ax2+bx+c=0的两根之和大于0; ②a+b<0;③y随x的增大而增大;④a-b+c<0,⑤2a-b>0. 其中正确的个数( ) 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.