题目内容
3．下表是2012年8月的日历：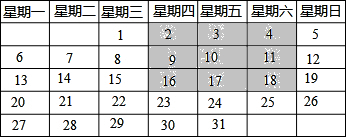
完成下列问题：
（1）图中方框（即阴影部分）的9个数的和是多少？它与方框中间的10有什么关系？
（2）方框中的三列数每一列的和是多少？有什么规律？
（3）方框中的三行数每一行的和是多少？有什么规律？
（4）把这个方框上下左右平移，得到新方框，若方框中间的一个数为a，则这个9个数的和为多少？
分析 （1）根据方框中的数字可以求和；计算可知9个数的和与10的关系；
（2）通过观察发现：上下相差7；和是中间数的3倍；
（3）通过观察发现：左右相差1；和是中间数的3倍；
（4）根据以上规律可发现方框上下左右平移，得到新方框中9个数的和与方框中间的一个数为a的关系与（1）中的规律相同．
解答 解：（1）9个数的和为2+3+4+9+10+11+16+17+18=90，这9个数的和是10的9倍；
（2）第一列的和为：2+9+16=27，第二列的和为：3+10+17=30，第三列的和为：4+11+18=33；每一列和是中间数的3倍；
（3）第一行的和为：2+3+4=9，第二行的和为：9+10+11=30，第三行的和为：16+17+18=51，；每一行和是中间数的3倍；
（4）把这个方框上下左右平移，得到新方框中间的一个数为a，则9个数的和为9a．
点评 本题考查的是数字的排列规律，解答本题的关键是根据表中的数字得出数字排列规律；此类题目经常考到，同学们注意掌握这类题目的解题思想．
练习册系列答案
阅读快车系列答案
相关题目
8．
如图，某飞机在空中A处探测到它的正下方地平面上目标C，此时飞行高度AC=1200m，从飞机上看地平面指挥台B的俯角α=30°，则飞机A与指挥台B的距离为（ ）
如图，某飞机在空中A处探测到它的正下方地平面上目标C，此时飞行高度AC=1200m，从飞机上看地平面指挥台B的俯角α=30°，则飞机A与指挥台B的距离为（ ）| A． | 1200m | B． | 1200$\sqrt{2}$m | C． | 1200$\sqrt{3}$m | D． | 2400m |
9．比-2015小1的数是（ ）
| A． | -2014 | B． | 2014 | C． | -2016 | D． | 2016 |
6．对于两个不相等的实数a、b，我们规定符号Max{a，b}表示a、b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{x，-x}=$\frac{2x+1}{x}$的解为（ ）
| A． | 1-$\sqrt{2}$ | B． | 2-$\sqrt{2}$ | C． | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D． | 1+$\sqrt{2}$或-1 |
13．
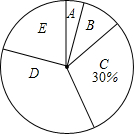今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：
（1）求全班学生人数和m的值．
（2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段．
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：（1）求全班学生人数和m的值．
（2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段．
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
| 分组 | 分数段（分） | 频数 |
| A | 36≤x＜41 | 2 |
| B | 41≤x＜46 | 5 |
| C | 46≤x＜51 | 15 |
| D | 51≤x＜56 | m |
| E | 56≤x＜61 | 10 |
在正方形ABCD内有一点P，且PA=2$\sqrt{2}$，PB=1，PD=$\sqrt{17}$，则正方形ABCD的边长为$\sqrt{13}$．
15．
如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为（ ）米．
如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为（ ）米．| A． | 7tanα | B． | $\frac{7}{tanα}$ | C． | 7sinα | D． | 7cosα |